Let $$a_n=\sum_{k=1}^{n}(\frac{1}{k})+\frac{1}{n+1}\binom{2n}{n}$$
I want to determine the generating function of $a_n$.
I could show that $$\binom{2n}{n}=(-4)^n(-1)^n\frac{1/2(1/2+1)(1/2+2)\dots(1/2+n-1)}{n!}=(-4)^n\binom{-1/2}{n}$$
using
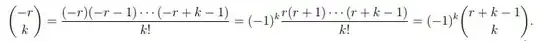 And we have that $$\sum_{n\geq0}\binom{-1/2}{n}(-4)^nz^n=(1-4z)^{-1/2}$$
And we have that $$\sum_{n\geq0}\binom{-1/2}{n}(-4)^nz^n=(1-4z)^{-1/2}$$
But I don't know how to arrive at (i.e. what to do with the factor $\frac{1}{n+1}$) $$\frac{1}{n+1}\binom{2n}{n}=\frac{1-(1-4z)^{1/2}}{2z}$$
The generating function of $$\sum_{k=1}^{n}\frac{1}{k}$$ should be $$\frac{z}{1-z}\cdot \underbrace{\sum_{n=1}^{\infty}\frac{z^n}{n}}_{={-\log(1-z)}}$$
or is this wrong?