1

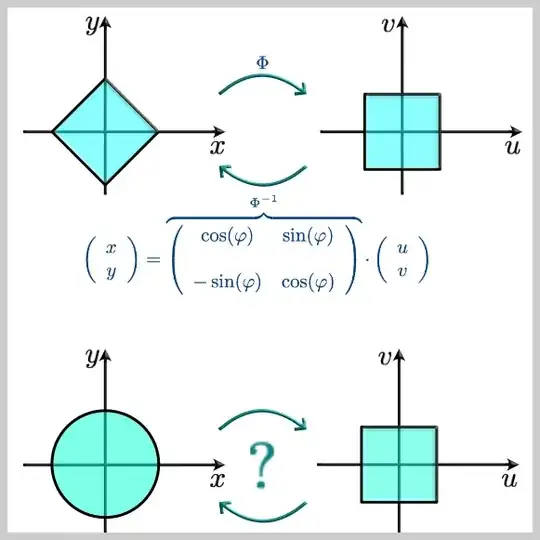
I'm striving for a general explanation of integral transformation. So far I've been told some variable substitutions (like polar coordinates) without really getting the gist of it. However I've just got to know a method that makes the whole process pretty clear to me due to matrix multiplication. That method I want to generalize:

enter image description here

So according to the the rotation transformation above I ask myself whether there exist something alike:

$\left(\begin{array}{cc}x\\y\end{array}\right) = \Phi \cdot \left(\begin{array}{cc}u\\v\end{array}\right)$ in order that $x = u\,\cos(v)\quad y = u\,\sin(v)$. Could it be?

Leon
  • 1,117
  • 1
    Here is a former answer of mine giving a solution in terms of a certain complex function connectd to elliptic integrals. – Jean Marie Apr 27 '21 at 10:22
  • 2
    With keywords sequence "mapping circle onto square" Google finds you a lot of references, some of them very simple. The advantage of conformal mapping is angle preservation. – Jean Marie Apr 27 '21 at 10:37

1 Answers1

1

A matrix represents a linear transformation. And a linear transformation maps lines onto lines. Hence no linear transformation will have the properties you ask for.

You need to look at other kind of transformations!

mathcounterexamples.net
  • 70,018