0

The $\varepsilon$-$\delta$ definition is: for a function $f: x \to f(x)$, the limit as $x$ tends to $a$ equals to $L$ as long as for every positve number $\varepsilon$, there exists a positive number $\delta$, such that if the distance between $x$ and $a$ (greater than 0) is less than $\delta$, then the distance between $f(x)$ and $L$ is less than $\varepsilon$.

To better illustrate what I mean, I've chosen this image below, where $x_{0}$ represents $a$. As you can see, it seems as if $L$ is a function of $a$

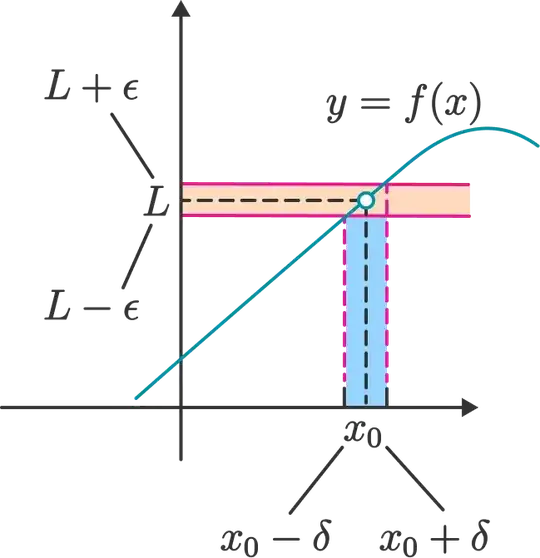
LfunctionofA

Epsilon-Delta Definition of a Limit. (n.d.). Brilliant. Retrieved April 23, 2021, from https://brilliant.org/wiki/epsilon-delta-definition-of-a-limit/

Xander Henderson
  • 29,772
Nameless
  • 415
  • Just because we don’t need to consider the case $x=a$ doesn’t mean the limit doesn’t depend on what $a$ is. We need to consider all $x$ such that $|x-a|<\delta$. What set that is depends on $a$, even if the set itself doesn’t include $a$. (However, it is true that the limit doesn’t depend on what $f(a)$ is. We can change the value of $f$ at $a$ to literally anything and provided the value of the function at all other points remains the same, we get the same limit.) – spaceisdarkgreen Apr 24 '21 at 04:20
  • @spaceisdarkgreen "We need to consider all $x$ such that $|x-a|$ $<$ $\delta$". By definition, wouldn't it be all such $x$ that $0$ $<$ $|x-a|$ $<$ $\delta$? Because if we only consider $0$ $<$ $\delta$ , it's pointless. That's what I think. – Nameless Apr 24 '21 at 04:43
  • Whoops, yes. That’s right. Point remains the same. – spaceisdarkgreen Apr 24 '21 at 04:49
  • 1
    I do not understand why you did the edit, without context of epsilon delta limits this question title is nonsense. What is $L$, what is $a$? – tryst with freedom Apr 24 '21 at 19:57
  • @Buraian The tags answer that question. Someone who has studied limits should be aware of the naming conventions such as $L$ and $a$. If not, the body of the question will answer it since I've provided the definition, which will explain what does each letter meam. – Nameless Apr 24 '21 at 20:00
  • 1
    Fine, that is understandable but why would you intentionally makes your question more difficult to understand in any way? @Nameless – tryst with freedom Apr 24 '21 at 20:01
  • @Buraian True, there's no reason. Thank you for noticing! I shall get rid of unneeded information. – Nameless Apr 24 '21 at 20:04
  • For the downvoter(s), please, could you provide a justification? I don't want make the same mistake the next time I ask a question. Thank you in advance. – Nameless Apr 24 '21 at 20:22
  • 1
    @Nameless You say that " Someone who has studied limits should be aware of the naming conventions such as $L$ and $a$." These are common conventions in undergraduate texts, but they are far from universally understood. It is better to write a title which gives more information and clarity. – Xander Henderson Apr 24 '21 at 23:00
  • @Xanderahenderson I find it redundant to be explicit when the question has been tagged with the topic and, in the question body, there has been given a definition. Although for non-users of this site, it's helpful. – Nameless Apr 25 '21 at 00:26
  • 3
    @Nameless I am sorry that you are troubled by redundancy. However, the title of the question is meant to convey a fair amount of information, as the tags are not displayed by (for example) the Google search engine. Moreover, as I pointed out above, the notation in your title is not necessarily standard or meaningful to everyone. Please also read the meta topic on titles. – Xander Henderson Apr 25 '21 at 01:15
  • @XanderHenderson Yes, it is reasonable to be explicit so others can search it up in, for example, the Google search engine. – Nameless Apr 25 '21 at 01:25

2 Answers2

0

we're approaching a

This notion of 'approaching' is only an informal way to understand. In the precise definition, it is not there. See wiki

Note that $x$ = {$(a- \delta, a + \delta) - a$}. That is, $x$ $\neq$ $a$ because we get 0 $<$ 0 $<$ $\delta$ , which is false, and $f(x)$ may be equal to $L$, according to the definition.

This part is kinda sketch, it is true that $x \neq a$ because we want $0< |x-a|<\delta$;notice the strict inequality.

Why? As far as I have understood, L is a function of a, we're approaching a and, as a consequence, we approach L.

I'd say the way you are thinking about it is brilliant here and has made me post my own question (see here). However, as far as 'standard' basic concepts go, the limit is informally dependent on the neighbourhood of 'a' rather than of that point 'a' itself.

I wouldn't personally call it a 'function' because it is non standard, a better way to say it would be to say that the limit is dependent of neighbourhood around 'a' rather than 'a' itself.

I'm asking this question because, from what've read, $f(x)$ can be equal to $L$. See Limits: why $f(x)$ can be equal to $L$ and $x$ can't be equal to $c$. Also, the book I'm working on also says $f(x)$ = {$(L - \varepsilon, L + \varepsilon)$}

Here it depends on your definition of $f(x)$ and it's kind of a subtle point. I had a similar doubt a long while back, have a look in this post.

tryst with freedom
  • 11,538
  • Thank you for your answer. I have a question regarding what you've said right here: "a better way to say it would be to say that the limit is dependent of neighbourhood around 'a' rather than 'a' itself". If we have $\lim_{a \to a_{1}}$ $=$ $L$ and $\lim_{a \to a_{2}}$ $=$ $L$ ($a_{1}$ and $a_{2}$ being different), $L$ is not necessarily the same in each limit. Thus, it depends on 'a' itself. Because of that, we can create a relation whose characteristics will, overall, yield a function – Nameless Apr 24 '21 at 19:16
  • I don't get your point , if $L$ is not the same how does that bring up any statements on the point I made about the limit value being a property of the nbhd? Here's a more explicit way of saying it, you can crank up $\delta$ to make the nbhds about $x$ bigger but all you need is a nbhd such that you get an epsilon delta relation to prove existence of the limit. My point on this is that, if you can prove so, then it must be that you there is some sufficiently sized interval such that the limit is provable if it exists – tryst with freedom Apr 24 '21 at 19:41
  • ". Because of that, we can create a relation whose characteristics will, overall, yield a function " I Don't get this point – tryst with freedom Apr 24 '21 at 19:43
  • @Burain What I tried to say is, the relation between $L$ and $a$ is such that it is possible to make $L$ a function of $a$. By the way, what does "nbhd" mean? Thank you in advance. Do you want me to edit my post so I can show you can what I mena by the statement you highlighted? – Nameless Apr 24 '21 at 19:44
  • Nbhd means neighbourhood, I think I got the problem now. I edited my answer, is it clearer now? @Nameless I think now that the way I described limit as being a function of nbhd may have been a bit confusing – tryst with freedom Apr 24 '21 at 19:47
  • No, my post and what I've said was: $L$ can be interpreted as a function of $a$, the limit value. – Nameless Apr 24 '21 at 19:50
-2

One way of thinking of this is $$\lim_{x\to a}f(x)=f(a)=L$$ So you can think of $L=f(a)$, indeed a function of $a$.

JayP
  • 1,096
  • Thank you for you answer. Does this mean that $f(x)$ $\neq$ $L$ ? – Nameless Apr 24 '21 at 04:19
  • That is correct. But it does approach $L$ as $x\to a$. I hope this helps! – JayP Apr 24 '21 at 04:20
  • 5
    This assumes that $f$ is continuous, which might not be the case. For example, the function $f$ which is defined so that $f(0) = 1$ and $f(x)= 0$ everywhere else has the property that $L(a) = \lim_{x\to a} f(x) = 0$ for all $a \in \mathbb{R}$, but $L \ne f$. – Xander Henderson Apr 24 '21 at 23:03