What is a parallel line?

Question

We are learning vectors in class and I have a question about parallel lines and coincident lines. According to wikipedia a parallel line is:

Two lines in a plane that do not intersect or touch at a point are called parallel lines.

But another reference says

Side by side and having the same distance continuously between them.

According to the above definition, you can have two parallel lines with a distance of zero but this contradicts the first definition. So which is it?

EDIT:

If it is the second definition then you can have two lines that are coincident and parallel right?

Answer 1

It's always important, in situations like this, to recall the immortal words of Humpty Dumpty (via Lewis Carroll's Through the Looking Glass):

"When I use a word, [...] it means just what I choose it to mean --- neither more nor less."

Indeed, Wikipedia's discussion of "Equivalent Properties" to Euclid's Parallel Postulate notes four "common definitions" of the term parallel: (1) constant separation, (2) never meeting, (3) same angles where crossed by some third line, or (4) same angles where crossed by any third line. (I'd say that (3) and (4) are slightly-nuanced ways of conveying the common notion of parallel lines "pointing in the same direction".)

Observe how these four "common definitions" apply to your "distance of zero" (aka, "coincident") lines:

1. Constant separation holds ... provided you allow that "separation by distance zero" counts as "separation". (That, too, is a choice.)
2. Never meeting fails: coincident lines meet everywhere.
3. Same angles where crossed by some third line holds: coincident lines are going to make identical angles!
4. Same angles where crossed by any third line holds: as in 3.

That's either 3-to-1 in favor of "coincident lines are parallel", or a 2-2 split decision; so the answer to your question "So, which is it?" is: It depends.

---

Personally, I'm a big fan of the "never meeting" definition of parallelism; it just seems the cleanest formulation. Number of points in common? Zero! Neat and tidy, whereas the other definitions involve a lot of extra work, measuring infinitely-many distances or at least a couple of angles. But, doggonit, it's just so convenient in algebraic geometry to say "lines with the same slope are parallel", or in linear algebra to say "vectors with the same (or proportional) components are parallel". My favorite trigonometric diagram has a nifty mnemonic that "reciprocal functions appear as parallel segments": $\sin \parallel \csc$ and $\cos \parallel \sec$; the "same direction" interpretation allows me to include $\tan \parallel \cot$ (and also $1 \parallel 1$), and it keeps the mnemonic from breaking down on a technicality at $0^\circ$ and $90^\circ$ when pairs of these "parallel" segments coincide. In the latter cases, being a stickler about "zero points in common" can get in the way of what's important about the situation.

The point is: One can make the case that coincident lines are parallel, and one can make the case the they aren't. Every day, mathematicians use the word "parallel" in ways that favor one choice over the other, and they freely change their minds depending on context. What they don't do, however, is leave their audience guessing on the matter, the way Humpty does to Alice. If there's potential confusion over any definition, a good mathematician gives explicit clarification about "what I choose [the word] to mean".

A common way of barring coincident lines from the Parallel Club is to be very vigilant to use the word "distinct" to describe the lines in question; that's why you see so many answers here making a big deal about the word. Another strategy is perhaps to use phrasing such a "strictly parallel" ... the latter being akin to describing a company's profit as "strictly positive", because somewhere someone might be asking this version of your question:

Can "profit" be zero?

Answer 2

The second definition--the equidistant property--is the definition with which most everyone is familiar... Euclid's 5th postulate.

However, in non-Euclidean geometry, parallel lines are not necessarily equidistant at all corresponding points. So the first definition is a more generalized definition.

In both definitions, parallel lines cannot intersect. I "assume" this is what was meant by the "side-by-side" reference in the 2nd definition. Since any line intersects itself at infinitely many points, then no, you cannot have coincident and parallel lines.

Answer 3

Basically, the first definition of two distinct lines are acceptable in three geometries we know, i.e; Euclidean, Spherical and Hyperbolic. I made the word distinct bold cause if two lines are not such that, so why are we working on them? If they are coincides, so does it have any senses we speak about two lines (They are one line and we don't want this case). So, we always assume that two lines are distinct and so speaking about zero distance doesn't make any senses. In Geometry, what you noted inside Edit shouldn't happen. Unless, in that case we are nothing to do with two lines.

Moreover about the second point you noted: I wanted to tell you this is true in Euclidean Geometry. This definition is absolutely wrong in other two geometries. In Hyperbolic, we have many many lines which are parallel to just one line asymptotically. And in Spherical one, we don't have any parallel lines!

Answer 4

The second defitinion is incomplete: two lines are parallel if they 1) do not intersect 2) maintain a constant separation between points closest to each other on the two lines. This second definition works for both two and three dimensional Euclidean space.

It is easy to visualize two parallel lines in two dimensions (a plane) as two lines that will never cross if extended infinitely; since they never cross, the first property (no intersection) is fulfilled. You'll also notice that the two lines maintain a constant distance apart.

Three dimensions is a little trickier, but not too bad. We live in three dimensions of space, so just imagine tying string from one wall of your room to another as a line. Obviously there are many ways to tie two different strings across your room that they don't intersect each other. (For example, tie your left/right walls together, and your front/back.) This is where the second property comes into play; two strings (lines) are parallel if when you pick any "starting" point on string $A$ and measure the shortest distance to string $B$ it equals the same distance as if you'd pick any other starting point. Think about why this holds for two dimensions, and you'll realize that the only way to achieve this in three dimensions is for the lines to lay in a plane. (For Euclidean {"standard"} space)

Your first definition only holds for two-dimensional space; it implies that the distance between them is constant, so it means the same as the [completed] second definition.

Answer 5

Lines are parallel iff they are distinct, non-intersecting, and not diverging. If you can travel along one of them arbitrarily far, and after some finite distance, any further travel will only make them get further apart, then they are diverging, and if not, they are parallel.

Lines that don't intersect are "non-secant". All parallel lines are also non-secant, and in 2D Euclidean geometry, all non-secants are parallel, but in 3D or Hyberbolic 2D, non-secant lines can be non-parallel.

A curve distinct from yet equidistant from a line (or something else like a point) is an Equidistant Curve. In non-euclidean geometry, equidistant curves to lines are never lines themselves. In 3D euclidean geometry, they may be, but might not be lines. Only in 2D euclidean geometry are equidistant curves to lines necessarily lines themselves.

Now for the really strange bit. Remember how parallel is defined in terms of moving along a line. That means being parallel has a direction. In Euclidean geometry, parallel lines are always parallel in both directions, but hyperbolic lines are only parallel in one direction, and they diverge in the other direction. So given a line, and a point not on that line, there are two parallel lines, one in each direction.

The following diagram shows a Poincare Disc model of the Hyperbolic plane. The points around the edge are "ideal points" while those within are real points. Hyperbolic lines map to circular arcs perpendicular to the edge of the disc.

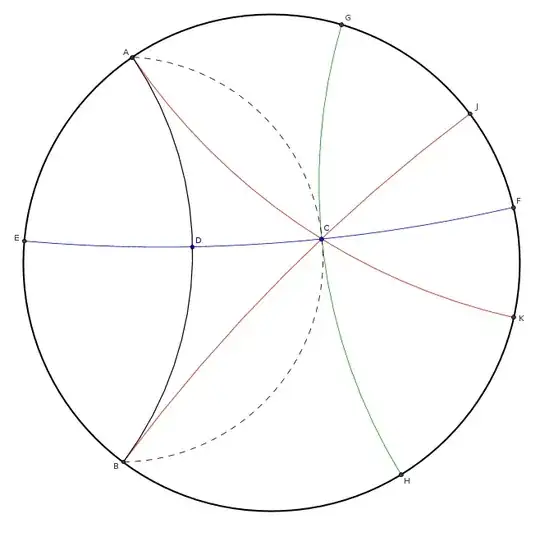
It hows Line $\overline{AB}$ and real point $C$. Perpendicular to $\overline{AB}$ through $C$ is $\overline{EF}$, and perpendicular to that through $C$ is $\overline{HG}$ which is nonsecant to $\overline{AB}$, but not parallel to it, note how they diverge to infinity in both directions. $\overline{AB}$ and $\overline{AK}$ are parallel, but only in the direction of ideal point $A$, they diverge toward $B$. Similarly, $\overline{AB}$ and $\overline{BJ}$ are parallel toward $B$. The dashed arc $\overset{\displaystyle\frown} {BCA}$ is actually an equidistant curve, not a line, note how it meets the edge of the dist at a non-right angle.