2

Let $ABC$ be a triangle. On the exterior of sides $AB$ and $AC$, construct two equilateral triangles $ABE$ and $ACF$. Let $H$ be the orthocenter of $ABC$ and $P$, $Q$ be the centers of $ABE, ACF$ respectively. I found out that $AH, EQ, FP$ are concurrent, and I remembered that it was a theorem in school geometry, but I couldn't prove it or find out its origin.

I also found (by GeoGebra) that: If $M, N$ are the midpoints of $AC, AB$ respectively then both $MP, NQ, AH$ and $EM, FN, AH$ are concurrent too, but I haven't proven it. Is this a well-known result in plane geometry?

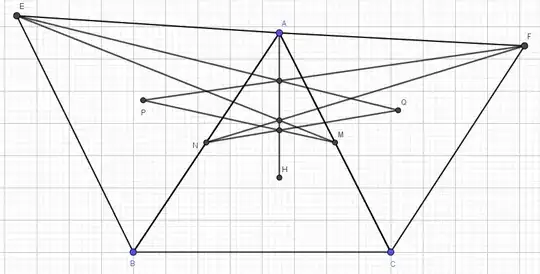
enter image description here

Please give me some hints or prove/disprove these results for me. Thanks

krazy-8
  • 2,224
anonimo
  • 439
  • 2
  • 8

3 Answers3

3

This is a very nice problem!

Lemma

Consider the following diagram, where we construct right triangles externally to an arbitrary triangle $\bigtriangleup ABC$. If $\;\measuredangle ABD=\measuredangle CBE \;$ and $\; BG \perp AC$; $$DC, BG, EA$$ are concurrent.

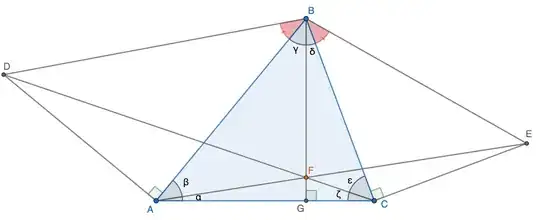
enter image description here

Proof.

Apply the law of sines on $\bigtriangleup CAD$ and $\bigtriangleup CBD$:

$$\frac{CD}{\sin(90°+\alpha+\beta)}=\frac{AD}{\sin \zeta} \tag{1}$$ $$\frac{CD}{\sin(\measuredangle ABD+\gamma+\delta)}=\frac{AD/(\sin\measuredangle ABD)}{\sin \epsilon} \tag{2}$$

Dividing $(1)$ by $(2)$:

$$\frac{\sin(\measuredangle ABD+\gamma+\delta)}{\sin(90°+\alpha+\beta)}=\frac{\sin \epsilon \cdot (\sin\measuredangle ABD)}{\sin \zeta} \tag{3}$$

Applying the law of sines on $\bigtriangleup ACE$ and $\bigtriangleup ABE$ we also get: $$\frac{\sin(\measuredangle CBE+\gamma+\delta)}{\sin(90°+\epsilon+\zeta)}=\frac{\sin \beta \cdot (\sin\measuredangle CBE)}{\sin \alpha} \tag{4}$$

Since $\bigtriangleup ABG$ and $\bigtriangleup CBG$ are right triangles:

$$\sin\gamma=\sin(\alpha+\beta) \;\; \text{and} \; \sin\delta=\sin(\epsilon+\zeta)\tag{5}$$

Dividing $(3)$ by $(4)$ and substituting from $(5)$:

$$\frac{\sin(\alpha)}{\sin(\beta)}×\frac{\sin(\gamma)}{\sin(\delta)}×\frac{\sin(\epsilon)}{\sin(\zeta)}= 1$$

Hence, by (Trigonometric) Ceva's theorem, the lines are concurrent. We note that this concurrency is independent of the measures of the angles $\measuredangle ABD$ and $\measuredangle CBE$ as long as they are equal.

Back to the original figure,

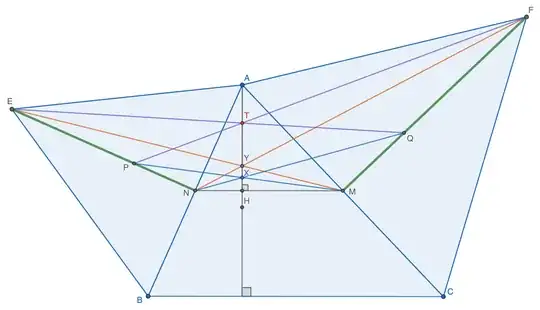
enter image description here

By the reverse of Thales' Theorem $NM \parallel BC$, so $AH \perp NM$. Construct the line segments $MP, AP, NQ, AQ\;$ and we get the desired configuration for our lemma (the main triangle being $\bigtriangleup AMN$). So, $MP, NQ, AH$ are concurrent. By similar constructions and using our lemma again both $EM, FN, AH$ and $EQ, FP, AH$ are also concurrent. $\; \blacksquare$

I suspect there is a simpler way to prove the Lemma (might be related to Jacobi's Theorem).

krazy-8
  • 2,224
  • 2
    Once you have your Lemma, you're done. After all, the Lemma implies that any "similarly-situated" points $U$ and $V$ on the perpendicular bisectors of $\overline{AB}$ and $\overline{AC}$ have the concurrency property. This includes the case of centers $U=P$ and $V=Q$ and the case of midpoints $U=N$ and $V=M$ (and also the case vertices $U=E$ and $V=F$, etc, etc, etc). – Blue Apr 29 '21 at 10:45
  • 1
    @Blue You are right, of course. Since my initial observation was to use Pappus’, I tried to force a solution using it. I totally neglected the fact that the Lemma trivializes all three concurrencies immediately. I edited accordingly, thank you. Any ideas on a geometric proof rather than using trigonometry to prove the Lemma? – krazy-8 Apr 29 '21 at 11:09
  • 1
    In the Lemma you surely meant "concurrent", not "collinear". – user Apr 29 '21 at 11:26
  • 1
    @dodoturkoz: At the moment, I don't see a trig-less approach that's any neater than your trig approach. Besides, the trig form of Ceva's Theorem needs more exposure. :) – Blue Apr 29 '21 at 11:35
  • 1
    @user I surely did! Thank you for the correction. – krazy-8 Apr 29 '21 at 14:37
  • 1
    @dodoturkoz Thank you very much for your nice solution. I know your lemma, but I forgot to use it. By the way, is this problem a well known theorem in elementary geometry? – anonimo May 08 '21 at 17:07
  • @dodoturkoz You could try to prove the lemma as follows: Let P be the intersection of the perpendicular line of AE, passing through C and BG. Then $AP\perp CD$, and F is the orthocenter of APC therefore CD, AE, BG are concurrent. – anonimo May 08 '21 at 17:16
  • 1
    @anonimo Sorry, I just noticed your response. To be honest, I have never seen this exact problem before, though concurrencies related to polygon constructions on sides of a triangle are extremely common. Here is a link to an extensive collection (BTW, I also don’t know French, but you can translate it easily) by the Frech geometer Jean-Louis Ayme: http://jl.ayme.pagesperso-orange.fr/Docs/Triangles%20adjacents.pdf – krazy-8 May 10 '21 at 09:51
  • 1
    @anonimo Regarding your proof: I feel a little tired now, but on the top of my head I couldn’t understand how you deduced $AP\perp CD$. If there is a simple explanation to it (maybe angle chasing), then you are right. This would be a much simpler proof than mine :) – krazy-8 May 10 '21 at 09:56
  • @dodoturkoz I can see from your proof that MP, NQ, AH and ME, NF, AH are concurrent but why EP, FQ, AH are concurrent? – trequartista Aug 08 '21 at 06:11
  • 2
    @trequartista Perhaps you have a typo; $EP, FQ, AH$ are not concurrent. – krazy-8 Aug 08 '21 at 08:15
  • @dodoturkoz Yes, I mean EQ, FP, AH. How can we deduce the proof for the concurrency of them by using your lemma? I think your lemma applies for MP, NQ and AH only. – trequartista Aug 08 '21 at 09:17
  • I can only use Pappus theorem for the case $EQ, FP, AH$ and looking for the more elementary proof. – trequartista Aug 08 '21 at 09:41
2

Welcome to MSE! This is vaguely related to the Fermat Point. Hope this helps.

BooleanCoder
  • 862
  • I felt that too, but I couldn't figure out that relationship. Could you please give me more details on that? – anonimo Apr 19 '21 at 07:07
1

Well, this should not be consider as an answer, but as a complement for the accepted answer of dodoturkoz, a more elementary proof for the lemma.

enter image description here

Let $K$ be the intersection of $BG$ and the perpendicular line of $AE$ passing through $C$.

Then, $\widehat{KCB}=\widehat{AEC}$.

Also $\widehat{KBC}=\dfrac{\pi}{2}+\widehat{ACB}=\widehat{BCE}+\widehat{ACB}=\widehat{ECA}$.

Thus the two triangles $KBC$ and $ACE$ are similar therefore: $\dfrac{KB}{AC}=\dfrac{BC}{CE}$.

On the other hand, $\Delta BCE\backsim \Delta BAD$, hence, $\dfrac{BC}{CE}=\dfrac{AB}{AD}$.

Thus $\dfrac{KB}{AC}=\dfrac{AB}{AD}$.

Moreover: $\widehat{KBA}=\dfrac{\pi}{2}+\widehat{BAC}=\widehat{BAD}+\widehat{BAC}=\widehat{DAC}$.

Therefore $\Delta KBA\backsim \Delta CAD$, and then $\widehat{BAK}=\widehat{ADC}$. Hence $CD\perp AK$.

As so, let $F$ be the intersection of $CD$ and $AE$, $F$ should be the orthocenter of $KAC$ and therefore $F$ is on $BG$.

Proof for the lemma is completed.

Arsenaler
  • 47
  • 1
    (+1) With so many given right angles, a proof involving the orthocenter of a triangle is of course more natural. Also, the way you used the proportionality of sides and congruency of the included angle to establish the final similarity is very nice. – krazy-8 Jun 18 '22 at 08:48