Angle chasing: Finding the $\angle{NRQ}$ in a quarter circle

Question

Let $MON$ be a quarter circle. $P$ is the midpoint of $OM$ and $PQ$ is the angle bisector of $\angle{OPN}$. If $QR\parallel{OM}$, find $\angle{QRN}$.

Here is an angle-chasing problem which I am trying to solve. I couldn't make a good progress solving the problem. Though here is my approach:

If we assume $\angle{OPQ}=\theta$ and $NP$ intersects $QR$ at $A$, then we have: $$\angle{OPQ}=\angle{NPQ}=\theta,$$ $$\angle{ONP}=\frac{\pi}{2}-\theta,$$ $$\angle{NAQ}=2\theta,$$ $$\angle{PQR}=\theta.$$So, $\Delta{PAQ}$ is isosceles.

This doesn't help very much. How to solve the problem?

Answer 1

WLOG, we can consider the circle as the unit circle.

Preliminary result: $PN=\dfrac{\sqrt{5}}{2}$ by Pythagoras in $\Delta OPN$.

Using the bisector angle theorem, we have, for a certain $k$:

$$\dfrac{QN}{QO}=\dfrac{PN}{PO}=\sqrt{5} \implies OQ=\dfrac{QN}{\sqrt{5}}$$

As $OQ+QN=1$ we must have

$$OQ=\dfrac{1}{2 \Phi}$$

where $\Phi=\dfrac{1+\sqrt{5}}{2}$ is the Golden Ratio.

As a consequence, using Pythagoras in triangle $\Delta OQR$:

$$OQ^2+QR^2=OR^2 \ \implies QR = \sqrt{1-\dfrac{1}{4 \Phi^2}}=\dfrac{1}{2 \Phi}a$$

where $a:=\sqrt{4 \Phi^2-1}=\sqrt{2 \sqrt{5}+5}=\dfrac{\sqrt{5}}{\sqrt{-2 \sqrt{5}+5}}$

$$\tan \angle QRN =\dfrac{QN}{QR}=\dfrac{\sqrt{5}}{2 \Phi \dfrac{1}{2 \Phi}a}=\dfrac{\sqrt{5}}{a}=\sqrt{5-2 \sqrt{5}}=\tan \dfrac{\pi}{5}$$

(see here); therefore:

$$\color{red}{\angle QRN = \dfrac{\pi}{5}}$$

Remark: I wouldn't be surprized that a simpler solution is found for example through a connection with the pentagram.

---

Edit: In fact (see my remark) my intuition is verified. Thanks to @user3236 this issue is like proving the validity of Richmond's construction. Here is another site with complementary informations: https://www.cut-the-knot.org/pythagoras/RichmondPentagon.shtml).

Answer 2

Here is a solution which tries to not use the algebraic knowledge of some trigonometric function (sine, cosine, tangent) of the angle of $36^\circ$ or some related angle (half or double of it). However, since there are "only a few" angles in the picture which are in measure a rational multiple of $\pi$, mainly those in $R$, we still need to involve some algebraic part.

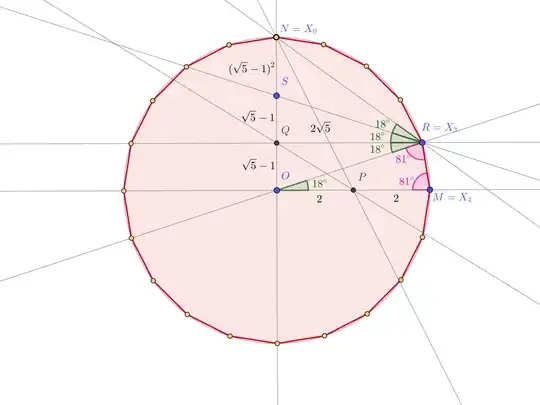
The idea is to show that the points $N,R,M$ from the OP are among the vertices of the $20$-gon. I will also use for them alternative notations $X_0$, $X_3$, and respectively $X_4$. To start with, let $S$ be the reflection of $O$ w.r.t. $Q$, so $OQ=QS$. I will work with a figure where the radius of the circle is $$ 4 = OM=ON\ . $$ Then $PN=\sqrt{2^2+4^2}=2\sqrt 5$, and in $\Delta NOP$ the angle bisector theorem gives $OQ:QN=2:2\sqrt 5$, so $\displaystyle\frac{OQ}4=\frac{OQ}{OQ+QN}=\frac2{2\sqrt 5+2}=\frac1{\sqrt 5+1}$, so $\displaystyle OQ=\frac 4{\sqrt 5+1}=\sqrt 5-1$. Some further computations are: $$ \begin{aligned} QS &= OQ=\sqrt 5-1\ ,\\ SN &= ON-2OQ=6-\sqrt 5=(\sqrt 5-1)^2\ ,\\ QR^2 &=OR^2-OQ^2=16-(5-2\sqrt 5+1)=10+2\sqrt 5=2\sqrt 5(\sqrt 5+1)\ ,\\ NR^2 &= QR^2+QN^2=(10+2\sqrt 5) + (5-\sqrt 5)^2=40-8\sqrt 5=8\sqrt 5(\sqrt 5-1)\ ,\text{ so}\\ \frac{NR^2}{QR^2} & = \frac{8\sqrt 5(\sqrt 5-1)}{2\sqrt 5(\sqrt 5+1)} = \frac{4(\sqrt 5-1)}{(\sqrt 5+1)} =(\sqrt 5-1)^2 =\left(\frac{NS}{SQ}\right)^2\ . \end{aligned} $$ The reciprocal of the angle bisector theorem (its usage here being the idea of this proof), insures now that the line $RS$ bisects the angle in $R$ in $\Delta QRN$. Let $x$ be the measure of $\widehat{ROM}$. Then we have the following situation with further angles computed in terms of $x$, using parallelism and an isosceles triangle:

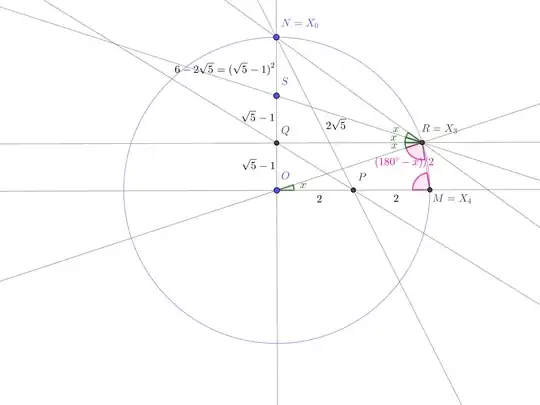
We obtain an equation involving $x$ from $$ 3x +\frac 12(180^\circ-x)=\widehat{NRM}=\frac 12\cdot (360^\circ-\overset\frown {MN})=\frac 12\cdot 270^\circ\ . $$ We double, and solving for $x$ in $6x+(180^\circ-x)=270^\circ$, we get
$$ \color{blue}{\boxed{ \qquad \begin{aligned} x &=\frac 15\cdot90^\circ=18^\circ\ ,\\ \widehat {QRN}&=2x =36^\circ \ . \end{aligned} \qquad}} $$ $\square$

---

We are done, but it may be a good impression to also see the $20$-gon in the picture...