Can $n$ hyperplanes separate any $\sum_{k = 0}^{m} \binom{n}{k}$ points in $\mathbb{R}^m$?

Question

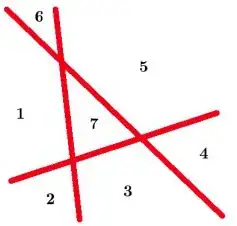
From this answer, we know that $n$ planes will partition $\mathbb{R}^m$ into a maximum of $N_{m,n} = \sum_{k = 0}^{m} \binom{n}{k}$ regions. Now we ask the reverse: given any $N_{m,n}$ points in general position in $\mathbb{R}^m$ do there always exist $n$ hyperplanes that will separate these points?

E.g. with $N_{2,3} = 7$ points in $\mathbb{R}^2$, the hypothesis is that there always exist $n = 3$ lines that completely separate any $7$ points.

enter image description here

if 7 points are colinear then you need 6 lines to separate them... — Dan Rust, Jun 03 '13 at 23:24

score 2 · Accepted Answer · answered Jun 04 '13 at 00:05

2

How about a regular heptagon? Each line has to separate the points into a group of three and a group of four. Two lines will give one isolated point and two pairs. But I can't find a third line to split all three pairs.

answered Jun 04 '13 at 00:05

Ross Millikan

374,822

Can $n$ hyperplanes separate any $\sum_{k = 0}^{m} \binom{n}{k}$ points in $\mathbb{R}^m$?

1 Answers1