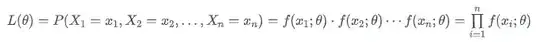There is given an i.i.d with this realisation: 0.481, 1.612, 1.755, 1.077.
The common density function of the above is:
\begin{array}{ll}
\frac{3x^2}{\vartheta^3} & \textrm{if } 0\leq x \leq \vartheta\\
0 & \textrm{otherwise.} \\
\end{array}
We have to determine the θ parameter with the ML estimation.
I know that we could use the above equation, but I can't see how could it help to solve the estimation. Or maybe should I use other technics?
\begin{align*} Likelihood(X_i|\vartheta) &= \begin{cases}\mathbb P(X=x_i | \vartheta)&if\, x_i<\vartheta\\0& otherwise\end{cases}\\ &= \begin{cases}\frac{3x_i^2}{\vartheta^3}&if\, x_i<\vartheta\\0& otherwise\end{cases}\\ \end{align*} Assume $\vartheta \geq max(\{x_1,\dots,x_4\})$ as we want to maximize likelihood and don't want the probabilities therefore to be 0.
Now we calculate the total likelihood. \begin{align*} Likelihood(\{X_1,\dots,X_4\}|\vartheta) &= \sum\limits_{i=1}^4 \mathbb P(X=x_i | \vartheta)\\ &=\frac{3\left(\sum\limits_{i=1}^4 x_i^2\right)}{\vartheta^3} \end{align*}
For maximizing likelihood, we set the derivative equal to 0 (to check for maxima of the function) \begin{align*} Likelihood(X_i|\vartheta^*) &= 0\\ -3\frac{3\left(\sum\limits_{i=1}^4 x_i^2\right)}{\vartheta^4}=0 \end{align*} But clearly the likelihood is always decreasing with increasing $\vartheta$ as the derivative is always negative (for $\vartheta \geq max(\{x_1,\dots,x_4\})$). Therefore we set it to the lowest possibile value where all the probabilities are positive.
$$\vartheta = max(\{x_1,\dots,x_4\}) = 1.755$$
