1

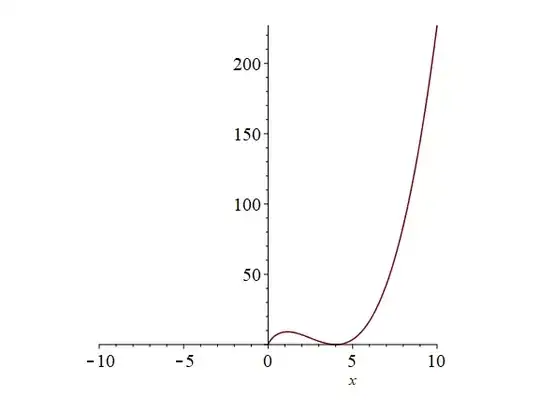
$f(x):=x^{4/5}\cdot (x-4)^2$

Maple gives me the graph:

enter image description here

WolframAlpha gives this graph

and my calculator gives Error 2 if I plug in $(-1)^{4/5}$.

My original intuition would be to think that the graph would be defined for negative $x$, but clearly something else is going on, what is going on in this case?

no lemon no melon
  • 2,129
  • 2
    fractional powers of negative numbers are not uniquely defined; cf. this question – J. W. Tanner Apr 16 '21 at 14:26
  • Wolfram likely interprets $x^{4/5}$ as $(x^4)^{1/5}$. In general, fractional powers of negative numbers are undefined over the reals. – Vishu Apr 16 '21 at 14:27
  • Many answers on this site give $(-1)^{4/5}=\left((-1)^4\right)^{1/5}=1^{1/5}=1=(-1)^4=\left((-1)^{1/5}\right)^4$ so in what way is it undefined?... @J.W.Tanner I'm reading the link currently as I'm typing this comment – no lemon no melon Apr 16 '21 at 14:34
  • Again, the numerator 4 is even while the denominator 5 is odd, so as P.Frost's answer states it is definable for this case, so it is undefined because in general fractional powers of negative numbers are undefinable? I don't get why I can't define it for this particular case – no lemon no melon Apr 16 '21 at 14:57
  • 1
    You're right that $x^{4/5}$ is a well-defined real-valued function on the real line. The question really is, why do Maple and your calculator not know this? It presumably comes down to respective algorithms for math libraries and when they throw NaN. You may have more luck on a computation-oriented site...? – Andrew D. Hwang Apr 16 '21 at 15:29
  • 1
    @AndrewD.Hwang I was reviewing curve sketching in Stewart Calculus and they go over a very similar function $f(x)=x^{2/3}(6-x)^{1/3}$ (Example 7, section 4.3, Calculus Early Transcendentals 7E) and they do in fact sketch the graph for $x<0$! The explanation they give (Example 7, Section 1.4) as to why some graphing calculators exclude graphing the function for $x<0$ is due to some machines compute roots using a logarithm, which is not defined for negative $x$. – no lemon no melon Apr 30 '21 at 20:02

0 Answers0