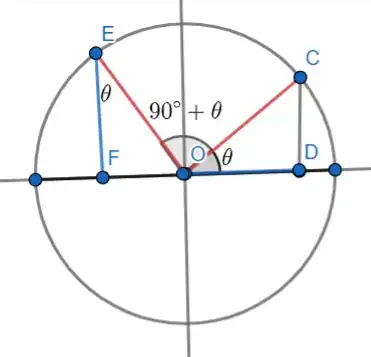
When finding trigonometric ratios for 90+theta. Why don’t we make the diagram like this ? I see we are not getting an angle of 90 degree. So , can’t we say there is no values of trigonometric ratio possible for 90+theta.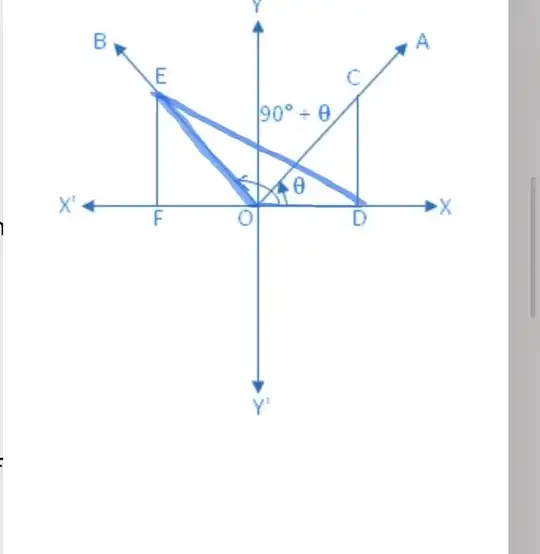
https://www.math-only-math.com/trigonometrical-ratios-of-90-degree-plus-theta.html. So , on this site I checked the proof for this. Below is the passage needed to understand this proof. What I didn’t get is how is sin theta = FE/OE
Take a point C on OA and draw CD perpendicular to OX or OX’.
Again, take a point E on OB such that OE = OC and draw EF perpendicular to OX or OX’.
From the right-angled ∆ OCD and ∆ OEF we get,
∠COD = ∠OEF [since OB ⊥ OA]
and OC = OE.
Therefore, ∆ OCD ≅ ∆ OEF (congruent).
Therefore according to the definition of trigonometric sign, OF = - DC, FE = OD and OE = OC
We observe that in diagram 1 and 4 OF and DC are opposite signs and FE, OD are either both positive.
Again we observe that in diagram 2 and 3 OF and DC are opposite signs and FE, OD are both negative.
According to the definition of trigonometric ratio we get, sin (90° + θ) = FE/ OE