Discrepancy calculating the distance between two opposite corners of a rectangle: infinite subdivisions vs hypotenuse

Question

I apologize in advance if this is a dumb question. I tried searching for duplicates but couldn't find any. Also, it is more of a curiosity, than a real question, so I hope it fits within the site guidelines.

Backstory

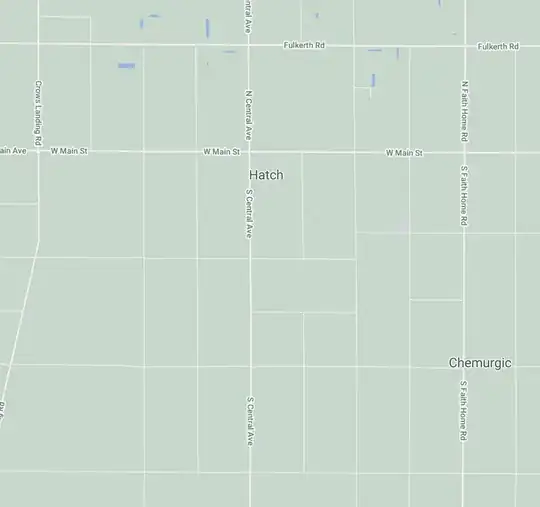
Yesterday, I was driving through California's Central Valley, thinking about how most of the roads there are orthogonal, directed north-south or east-west, creating some sort of square grid. Similar pattern to one found in many American cities and towns, with square grid layouts.

Here is a snapshot from Google Maps near Turlock, CA

I had driving directions on, and wondered for a bit about how an algorithm would calculate the shortest/fastest path when traveling "diagonally" (northeast -> southwest, for example). I didn't spend too much time on that, since some of these roads have different features, speed limits, etc.

Instead, I started thinking about different ways to calculate the distance between opposite corners of a square or rectangle (for simplification, I will focus on squares moving forward, but the math applies to both).

Pythagoras

We know that using Pythagoras, we can calculate the hypotenuse as the square root of the sum of the sides squared:

$ h = \sqrt{a^2 + b^2} $

Thus, for a 10 by 10 square, the hypotenuse will be the square root of 200: 14.1421...

Not Pythagoras

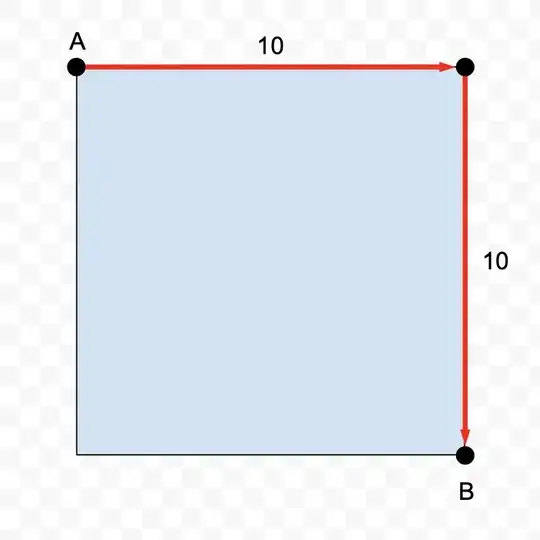
Ok, now, consider this. Given a 10 by 10 square (think of a city block, or orthogonal roads like the ones above), if we want to travel from one corner (A) to the opposite corner (B), first we need to visit one of the remaining two corners.

In this case, the distance traveled would be 10 + 10 = 20 (much longer than the 14.14 hypotenuse).

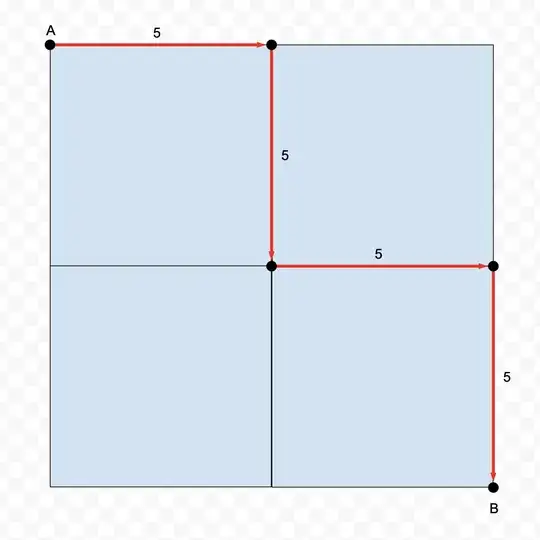
Now, if we divide this square into 4 equal squares, and we travel through the center, the distance traveled will remain the same: 5 + 5 + 5 + 5 = 20 units.

The number of horizontal segments is equal to the number of columns (2 in this case).

The length of each horizontal segment is equal to the width divided the number of columns:

$ s_h = \frac{width}{columns} $

Thus, the distance traveled horizontally $ d_h $ would be $ s_h * columns $, or in other words, equal to the total width.

The same applies to the distance traveled vertically $ d_v $, where the total distance will be equal to the total height.

$ d_h = columns * \frac{width}{columns} = width $

$ d_v = rows * \frac{height}{rows} = height $

It seems to be the case that the number of columns and rows does not matter, as the distance traveled will always be the sum of the width (horizontal distance) and height (vertical distance).

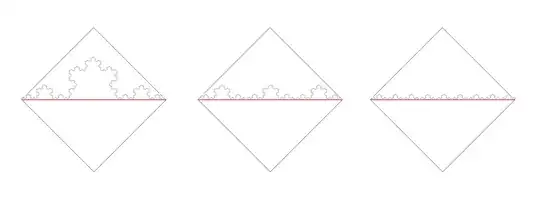
We could divide the square infinitely, so we have infinite columns and infinite rows, and the distance will still be the same (20 units in this example).

Wait a minute...

My Conjectures

1. According to the above, the distance traveled through infinite segments will be 20.

2. Why is the value so different from the hypotenuse (almost 50% higher), given than the path from A to B would pretty much represent a diagonal line at that point?

It's been long since I studied integrals and Calculus, so I'm looking for someone that would not mind spending some time explaining this.

Thank you!

PS: I looked at this question, which has a nice diagram similar to mine, but the Manthatan Distance (aka Taxicab Geometry) is not what I'm looking for, as it does not mention any relation with hypotenuse distance when the number of segments approaches infinity.

Answer 1

What you say about dividing it into line segments is true, so long as you restrict it to finitely many line segments. the mistake you are making, and it is a very common one, is to assume that what is true of finitely many segments remains true when we somehow jump to infinitely many many segments.

In the first place, it isn't clear at all what you mean by infinitely many segments. How exactly is the distance to be divided into infinitely many segments. In the finite examples you give, all the segments are the same size, but if we have infinitely many segments of the same size, their total length will be infinite.

Leaving that problem aside for the moment, there is no reason to believe that because the lengths of the staircase curves is constant, the limit of these curves will have the same length. If you think about how arc length was defined in calculus, as the supremum of the lengths of all possible inscribed polygonal paths, you'll see it has nothing to do with these staircase curves, which are not inscribed in the diagonal. Furthermore, it is not true that familiar properties are preserved by passage to the limit. On the contrary, a great deal of effort has been spent in discovering conditions under which the limit of a sum is the sum of the limits, the limit of an integral is the integral of the limits, and so on.

As to your final point, "The path from A to B would pretty much represent the hypotenuse at that point," no it wouldn't. As you yourself have pointed out, it's almost $50\%$ longer.

Answer 2

As @saulspatz points out, this paradox illustrates an issue with our intuition, not an issue with our definition of length.

If I have a sequence of paths $\gamma_n: [0, 1] \to \Bbb{R}^2$ connecting two points $P$, $Q$ (i.e. $\gamma_n(0) = P$, $\gamma_n(1) = Q$ for all $n$), and this sequence of paths converges pointwise to another path $\gamma: [0, 1] \to \Bbb{R}^2$ connecting $P$ and $Q$ (i.e. $\gamma(0) = P$, $\gamma(1) = Q$), then the arclengths $L_n$ of the paths $\gamma_n$ need not converge to the arclength $L$ of the limiting path $\gamma$.
We would need additional assumptions, such as that the paths $\gamma_n$ and $\gamma$ are smooth (i.e. continuously differentiable) curves for which $\gamma_n'(t) \to \gamma'(t)$ pointwise (in addition to $\gamma_n(t) \to \gamma(t)$ pointwise), to conclude that $\lim_{n \to \infty} L_n = L$.
(Although Fatou's lemma does guarantee that $\liminf L_n \geq L$--that is, if the $L_n$ converge but not to $L$, they have to converge to something bigger, not smaller, than $L$. We couldn't make up an example like this where the lengths of the diagonal approximations converged to a limit smaller than the diagonal, in other words. Informally, we interpret this as saying the extra bumpiness/jaggedness in cases of non-convergence always increases the sequence of arclengths, compared to the limiting curve’s arclength.)
In the OP example, the "street grid" paths $\gamma_n$ have corners (in fact, more and more corners as I make the gridlines closer and closer together) while the "crow-flight" diagonal path itself is smooth, and that jaggedness is what keeps those lengths from settling down to the diagonal length.

It may interest you to know that this isn't even the most pathological example out there. We could use the fractal Koch curve, which is infinitely long (and infinitely jagged), to build a sequence $\gamma_n$ of approximations to the diagonal of the square, each of which has infinite length: But as explained previously, this picture should not be interpreted as saying that the diagonal of the square is infinitely long!

Answer 3

The length of the hypoteneuse on a right triangle with sides $a,b$ is $\sqrt{a^2+b^2}$.

In this case, we have $a=b$, and the limit of the ratio tends:

$$\lim_{a\to0} \frac{2a}{\sqrt{2a^2}}=\sqrt{2}$$