How to find the $\sum_{i=0}^n{\ell+i\choose i}$. I'd tried several binomial series, but cannot be work. Also does it have a combinatoric intuitive explanation?
Asked
Active
Viewed 74 times
0
-
There is no identity here. An identity has an equal sign in it. What are you trying to prove? – saulspatz Apr 10 '21 at 15:15
-
What is the identity that you wish to prove? The expression you have written is not an identity. – Dilip Sarwate Apr 10 '21 at 15:15
-
Oops, sorry about that. Just editted. I was thinking that there is an identity.. – Shara Apr 10 '21 at 15:17
-
1Try using https://en.wikipedia.org/wiki/Hockey-stick_identity. Or you can write out a few terms and induct. Hint: It's equal to one binomial, something choose $n$. – TheBestMagician Apr 10 '21 at 15:18
-
An alternative hint: try using the diagonals of Pascal's triangle – Sofía Marlasca Aparicio Apr 10 '21 at 15:23
-
@marlasca23 Hockey stick gets its name from the diagonal of Pascal's triangle. They are the same thing, I believe. – TheBestMagician Apr 10 '21 at 15:24
1 Answers
2
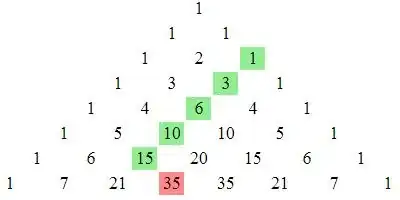
Consider the image
The famous demonstration of the hockey stick identity. With your sum, we can start at $\binom{\ell}{0}$ and take a walk down the diagonal for $n$ terms (its the mirror image of the above picture). By the hockey stick identity, this is simply $\binom{n+\ell +1}{n}$. This is because the last term is $\binom{\ell +n}{n}$, then we go to the next row, to $\binom{\ell +n+1}{n}$ for the sum.
TheBestMagician
- 2,864