1

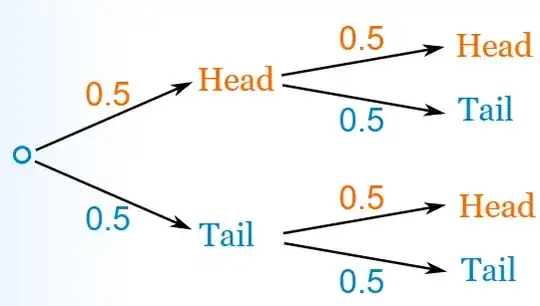
I'm trying to reason about the following question:

Given two fair coins, what is the probability of the event both coins land heads-up conditional on the event "at least one of the coins lands heads-up?"

Is it possible to use a simple tree diagram to calculate the answer?

enter image description here

Part of my problem is understanding the tenses of the events, and the probability evaluation.

Are we talking retrospectively? Or after just one coin has landed, what the probability is in terms of predicting the second one? This seems problematic as we can't know whether at least one coin landed heads-up until both have been flipped.

I know the answer is "supposed" to be 1/3, as from the permutations where at least one coin lands heads-up: {HH, HT, TH}, only one is the desired result.

However, something doesn't add up for me and I end up going round in circles whenever I try to make sense of the question. Any clarification would be much appreciated.

Robin Andrews
  • 957
  • Maybe it will be clearer if you just follow the standard definition of conditional probability. You want $\frac {P(E_1\cap E_2)}{P(E_2)}$ where $E_1$ is the event "both coins are $H$" and $E_2$ is the event "at least one coin is $H$". Clearly $E_1\cap E_2=HH$ And $P(E_2)=\frac 34$. – lulu Apr 10 '21 at 10:51
  • But, really, there's nothing wrong with your argument. If you start with four equally probably outcomes and someone excludes one of them with no further information, then you still have nothing with which to distinguish the remaining cases so your prior is that they too are equally probable. – lulu Apr 10 '21 at 10:53
  • 1
    Thanks. I'm reluctant to use the formula because I don't fully understand it (now may be a good time to address that). However I was tempted to make my question more focused on the how the problem can be understood in terms of the tree, as it seems possible to impose a time-sequence on this which would highlight my overarching confusion about the "when" of the events and probability evaluations. – Robin Andrews Apr 10 '21 at 10:57
  • Not following. I don't see how time enters into this. Say an urn contains four balls (one White, one Black, one Red, one Blue, otherwise indistinguishable). You draw one without looking. Someone else tells you that it is not Blue. Then what is the probability that it is Red? This is the same question (why?). – lulu Apr 10 '21 at 11:07
  • To stress: it is a very different problem if you ask "Suppose I toss a fair coin and get $H$. Then I toss another fair coin. What is the probability that in the end I have $HH$." The answer to that question is $\frac 12$ since it just comes down to the second toss. – lulu Apr 10 '21 at 11:16
  • @lulu As far as I can tell, time comes in to it because if we are discussing the situation after both coins have been flipped (which must be the case if we know for sure that one is heads), then I don't see how learning the new information that at least one coin was heads can retrospectively change the probability of HH, which was originally 1/4. – Robin Andrews Apr 10 '21 at 12:16
  • But of course new information can change your view of the probability. If you were told "at least one of hem came up $T$" then you would see that the probability that they were $HH$ was $0$. – lulu Apr 10 '21 at 12:37
  • One way to interpret this is to say that, having been tossed, the probability that it is $HH$ is, in reality, either $1$ or $0$, since the toss is complete. But since you do not know the outcome, what matters is your view of the probability. That's why you and I can attach different probabilities to the same event. I, knowing nnothing at all about the outcome, think the answer is $\frac 14$. You, knowing only that $TT$ is excluded, think it is $\frac 13$, person $X$ ,knowing that the first coin came up $H$, thinks it is $\frac 12$.... – lulu Apr 10 '21 at 12:40
  • ...while someone who has seen both coins knows the outcome for a certainty. None of these views is "wrong" but each successive view is based on having more information. – lulu Apr 10 '21 at 12:41
  • This is messing with my head. Is it the case that the correct answer to the original question is "undefined", since the amount of available information has not been specified? – Robin Andrews Apr 10 '21 at 17:34
  • No. the answer is $\frac 13$. Aside from knowing that these were two fair tosses of fair coins, the extra information is that at least one came up $H$. I don't see any ambiguity. – lulu Apr 10 '21 at 17:37
  • @RobinAndrews maybe you are confused by the tree that you drew. In that case I propose a modification to the tree. On the right side, please write out the outcomes as ${HH,HT,TH,TT}$ Then you can see again that there are four events in all, and after conditioning (on atleast 1 head) three equivalent outcomes remain. – Rahul Madhavan Apr 10 '21 at 21:51

0 Answers0