I ask for help in mathematicians, specialists in the theory of differential equations.
$\frac{dx}{dt}=\frac{d}{dx}f(x)$
where $f(x)$ - unknown unimodal function. For example: $f(x)=−(x−x_∗)^2$ or $f(x)=e^{(−(x−x_∗))^2}$
About convergence:
If we substitute such a function into the equation $\frac{dx}{dt}=\frac{d}{dx}f(x)$, then the solution will always converge from the initial point $x(0)$ to the one at which the extremum of the function is reached, i e. $x_∗$
Assumptions:
Suppose we know that $f(x)$ is unimodal, but we do not know the position of the maximum/minimum (we do not know $x_∗$).
It is assumed that the steady-state of the system exists, but it is not known in advance.
Question: How to create exponential rate convergence in such a system?
I will illustrate the dynamics on the example of the function $f(x)=e^{(−(x−x_∗))^2}$ and what I need to get. There is my code in Mathematica:
Clear["Derivative"]
ClearAll["Global`*"]
pars = {xstart = -1, xend = 1}
f = Exp[-(x[t] - xend)^2]
sys = NDSolve[{ x'[t] == D[f, x[t]], x[0] == xstart}, {x}, {t, 0, 500}]
Plot[{Evaluate[x[t] /. sys], xend}, {t, 0, 300}, PlotRange -> Full,
PlotPoints -> 100]
What I have ($x_*=1, x(0)=-1$)
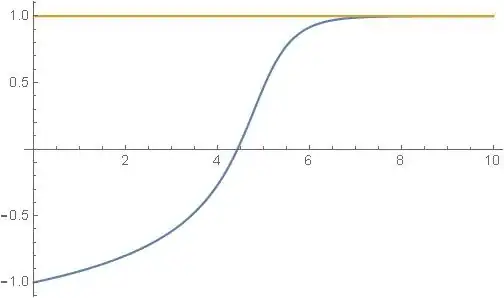
What I have ($x_*=-1, x(0)=1$)
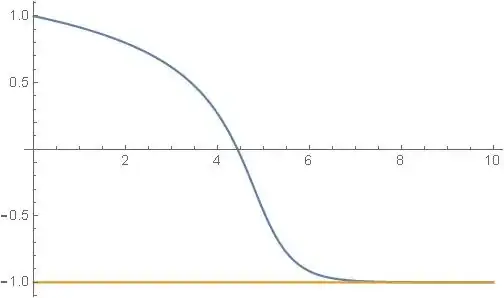
Let me remind you to assumption: we do not know the position of the extremum and the structure of the function, but we know that it is unimodal (has a maximum or a minimum)
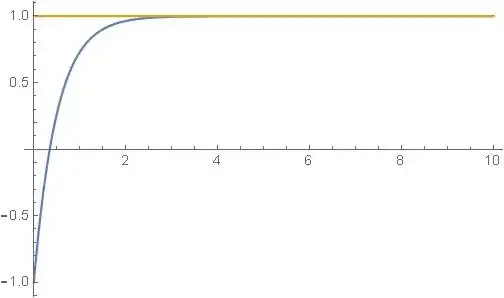
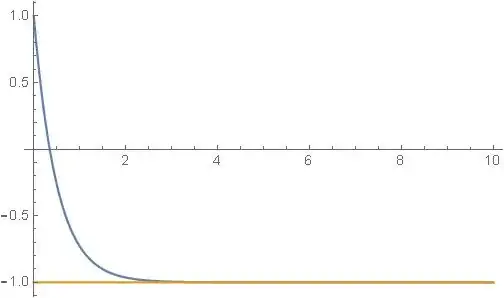
Please, see my new question:
https://math.stackexchange.com/questions/4096460/problem-with-the-continuous-equivalent-of-newtons-method-optimization
– dtn Apr 10 '21 at 05:43