1

The question is

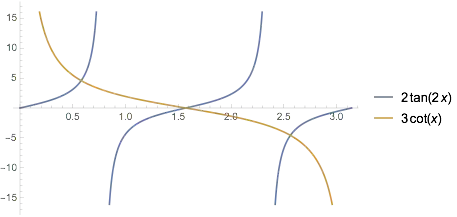
Find the solutions to the equation $$2\tan(2x)=3\cot(x) , \space 0<x<180$$

I started by applying the tan double angle formula and recipricoal identity for cot

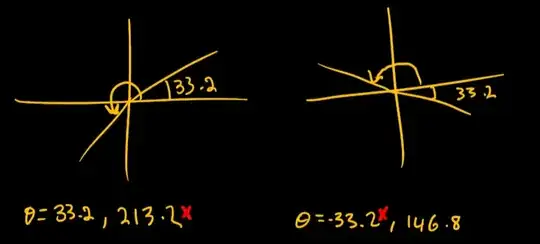
$$2* \frac{2\tan(x)}{1-\tan^2(x)}=\frac{3}{\tan(x)}$$ $$\implies 7\tan^2(x)=3 \therefore x=\tan^{-1}\left(-\sqrt\frac{3}{7} \right)$$ $$x=-33.2,33.2$$

Then by using the quadrants quadrant

I was lead to the final solution that $x=33.2,146.8$ however the answer in the book has an additional solution of $x=90$, I understand the reasoning that $\tan(180)=0$ and $\cot(x)$ tends to zero as x tends to 90 however how was this solution found?

Is there a process for consistently finding these "hidden answers"?

amWhy
  • 209,954
Filthyscrub
  • 592
  • 3
    $\cot$ doesn't "tend" to $0$ at $90^\circ$. It is zero at $90^\circ$. – Arthur Apr 07 '21 at 15:22
  • 3
    Presumably, you miss that solution when you write everything in terms of $\tan x$ because that assumes that $\tan x$ is actually defined. You have to consider the possibility when $\tan x$ is undefined, i.e. when $x=(90+180n)^\circ$ – Vishu Apr 07 '21 at 15:22
  • 3
    You introduced $\frac1{\tan(x)}$ and $\frac1{1-\tan^2(x)}$ and then multiplied both sides of the equation by $\tan(x)(1-\tan^2(x))$ so may have to check cases where $\tan(x)=0,\pm1,\infty$ – Henry Apr 07 '21 at 15:24
  • 2
    If you know what the missing solution is, and you want to know how it disappeared, a good idea is usually to insert that value into different steps in the calculation and see what happens to that solution at different stages. – Arthur Apr 07 '21 at 15:28
  • 1
    The "missing" solution was removed by overzealous cancellation of terms. It's like if you were given the polynomial equation, $x(x-1)=x$, you would lose the solution $x=0$ if you cancel factors of $x$ on either side to end up with $x-1=1$. (In fact, this cancellation is only ever valid if $x\neq0$.) The proper thing to do would be to move everything to one side, then factor: $x(x-1)-x=0$, followed by $x(x-1-1)=x(x-2)=0$. – user170231 Apr 07 '21 at 15:39

7 Answers7

2

$$\frac{4\tan(x)}{1-\tan^2(x)} = \frac{3}{\tan(x)}$$

$$\frac{4\tan(x)}{1-\tan^2(x)} - \frac{3}{\tan(x)} = 0$$

$$\frac{4\tan^2(x)-3[1-\tan^2(x)]}{\tan(x)[1-\tan^2(x)]} = 0$$

$$\frac{7\tan^2(x)-3}{\tan(x)[1-\tan^2(x)]} = 0$$

You focused in the fact that the equation is satisfied when the numerator is zero, i.e., $7\tan^2(x)-3=0$, but the equation is also satisfied when $\tan(x)\to\infty$ (when the denominator itself tends to infinity).

$$\lim_{\tan(x)\to\infty} \frac{7\tan^2(x)-3}{\tan(x)[1-\tan^2(x)]} = \lim_{\tan(x)\to\infty} \frac{\tan^2(x)\left[7-\frac{3}{\tan^2(x)}\right]}{\tan^2(x)\left[\frac{1}{\tan(x)}-\tan(x)\right]} = \lim_{\tan(x)\to\infty} \frac{7-\frac{3}{\tan^2(x)}}{\frac{1}{\tan(x)}-\tan(x)} = 0$$

Zalnd
  • 586
2

Find the solutions to the equation
\begin{align} 2\tan(2x)=3\cot(x),\quad 0^\circ<x<180^\circ \tag{1}\label{1}\end{align}

As it was already noted, $\tan x$ is not defined on the whole range $(0^\circ,180^\circ)$, but $\cot x$ is, so if we use it instead in \eqref{1}:

\begin{align} \frac2{\cot 2x}&=3\cot(x) ,\\ \frac{4\cot x}{\cot^2 x-1} &= 3\cot x , \end{align}

we get the missing third solution, $\cot x=0$.

g.kov
  • 13,581
2

The error is in your very first line.

As alluded to by @Tavish in the comments, since the double-angle identity for $\tan$ has domain $$\mathbb R\setminus \left\{(2k+1)\frac{\pi}2 \mid k\in\mathbb Z\right\},$$ a separate case for odd multiples of $90^{\circ}$ ought to be created when applying it. (In doing so while solving an equation where the flow of logic is $“\implies”$ rather than $“\iff”,$ we are merely asserting that this separate case contains potential solutions.)

  • So, for $x\in\left(0^{\circ},180^{\circ}\right),$

    $$2\tan(2x)=3\cot(x) \tag1$$ $$\implies \frac{4\tan(x)}{1-\tan^2(x)}=\frac{3}{\tan(x)} \quad\text{or}\quad x=90^{\circ} \\ \implies \tan^2(x)=\frac37 \quad\text{or}\quad x=90^{\circ}$$ $$\implies x=33.2^{\circ}\:\text{or}\:146.8^{\circ} \quad\text{or}\quad x=90^{\circ}; \tag2 $$ plugging (2) into (1) reveals that the full solution set is $\left\{33.2^{\circ},90^{\circ},146.8^{\circ}\right\}.$

  • Alternatively, using “$\iff$”:

    for $x\in\left(0^{\circ},180^{\circ}\right),$

    $$2\tan(2x)=3\cot(x) \\ \iff \left[\frac{4\tan(x)}{1-\tan^2(x)}=\frac{3}{\tan(x)} \quad\text{or}\quad x=90^{\circ}\right] \quad\text{and}\quad \cos(2x),\sin(x)\neq0\\ \iff \left[\tan^2(x)=\frac37 \quad\text{or}\quad x=90^{\circ}\right] \quad\text{and}\quad \cos(2x),\sin(x)\neq0\\$$ $$\iff x=33.2^{\circ}\:\text{or}\: 90^{\circ}\:\text{or}\: 146.8^{\circ}.$$

ryang
  • 38,879
  • 14
  • 81
  • 179
1

In your second equation, the only way you can get from that equation to $7\tan^2{x} = 3$, is by assuming that $\tan{x}$ and $1 - \tan^2{x}$ is not equal to $0$ or infinity because you can't divide by $0$ or infinity. But the hidden case is that $1 - \tan^2{x} = 0$ or infinity or that $\tan{x} = 0$ or infinity.

We only see that one case works, and it is when $x = \boxed{90}$ degrees.

I am a person
  • 1,084
1

Perhaps this graph will help reveal the answers (abscissa in radians):

enter image description here

David G. Stork
  • 29,774
1

The moment you substitute $\cot x\mapsto \frac1{\tan x}$, you are implicitly assuming that $x\neq 90^\circ$, because that's required for that substitution to make sense. So that's a case you have to manually check in the original equation because it might be a solution that disappears (and in this case it indeed turned out to be a solution that disappears).

Arthur
  • 199,419
1

Factorize the equation as follows

\begin{align} 2\tan(2x)-3\cot(x) =& \frac{2\sin2x}{\cos 2x} - \frac{3\cos x}{\sin x}\\ =& \frac{2\sin2x\sin x-3 \cos x\cos2x }{ \sin x\cos 2x}\\ =& \frac{\cos x(10\sin^2x-3 )}{ \sin x\cos 2x}\\ \end{align} where the factor $\cos x =0$ captures the solution $x=\frac\pi2$ and $10\sin^2x -3=0$ yields $x= \sin^{-1}\sqrt{\frac3{10}}, \>\pi - \sin^{-1}\sqrt{\frac3{10}}$.

Quanto
  • 97,352