-2

I want to compute the derivative of the distribution of $X|(X+Y=u)$.

Aaron Hendrickson
  • 6,042
John
  • 1
  • There are standard ways to get the distribution function for the sum of independent random variables. Convolution or using characteristic function (Fourier transform). – herb steinberg Apr 04 '21 at 16:49
  • Could please you go into detail how you would do this? Many thanks in advance, John – John Apr 04 '21 at 16:52
  • Assuming the density functions exist with $Z=X+Y$ then $f_Z(z)=\int f_X(x)f_Y(z-x)dx$. Using char. function: $\phi_V(t)=\int f_V(x)e^{itx}dt$ then $\phi_Z(t)=\phi_X(t)\phi_Y(t)$ and $f_Z(z)=\frac{1}{2\pi}\int\phi_Z(t)e^{-itz}dt$. If the density function does not exist, you need to use Stieltjes integral of the distribution function. There are similar expressions for discrete distributions. – herb steinberg Apr 04 '21 at 17:04
  • Hints: (a) $S = X + Y \sim \mathsf{Pois}(\lambda_1+\lambda_2).$ (b) $P(X=x|S=u) = $ $\frac{P(X=x,S=u)}{P(S=u)}=$ $\frac{P(X=x,Y=u-x)}{P(S=u)} =$ $\cdots$ $ {u\choose x}p^x(1-p)^{u-x},$ where $u > x, p = \frac{\lambda_1}{\lambda_1+\lambda_2}.$ – BruceET Apr 04 '21 at 17:35

1 Answers1

1

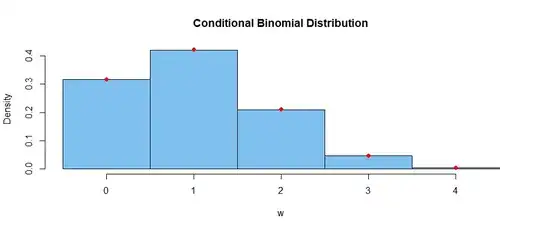
Comment continuted: Simulation in R for $\lambda_1 = 1; \lambda_2 = 3, u = 4.$

lam.1 = 1;  lam.2 = 3,  u = 4
p = lam.1/(lam.1+lam.2)
set.seed(404)
x = rpois(10^6, lam.1)
y = rpois(10^6, lam.2)
s = x + y
w = x[s ==u]      # [ ] denotes conditioning
mean(w); var(w)
 [1] 1.000098     # aprx E(W) = up = 4(1/4) - 1
 [1] 0.7502605    # aprx Var = 3/4

hdr = "Conditional Binomial Distribution"
hist(w, prob=T, br=(0:5)-.5,col="skyblue2", main=hdr)
 k = 0:4;  pdf = dbinom(k, 4, p)
 points(k, pdf, pch=19, col="red")

enter image description here

BruceET
  • 51,500