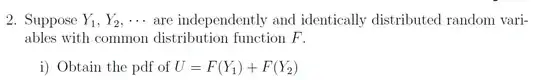Density Function of $F\left(Y_1\right)+F\left(Y_2\right)$

Question

I came across a question which stated:

Suppose $Y_1,Y_2,...$ are independently and identically distributed random variables with common distribution function $F$. Then find the pdf of $$U=F\left(Y_1\right)+F\left(Y_2\right)$$

From what I understood of the question, I proceeded as follows (which, I assume, is not correct as I couldn't understand the question properly):

I tried to find the CDF of $U$ and I wrote this $$\begin{align}P\left(U\leq u\right)&=P\left(F\left(Y_1\right)+F\left(Y_2\right)\leq u\right)\\ &=\int_0^1P\left(F\left(Y_1\right)+y_2\leq u\right)\cdot P\left(F\left(Y_2\right)\leq y_2\right)\cdot dy_2\\ &=\int_0^1\left(F\left(Y_1\right)\leq u-y_2\right)\cdot\left(F\left(Y_2\right)\leq y_2\right)\cdot dy_2 \end{align}$$ I cannot go any further and am confused as to how this problem can be done. Any suggestions and hints will be very much helpful.

Some thoughts crept into my mind as I was writing this down here: Suppose I take another random variable (say $X$) such that I can write the above integral as $$\int_0^1\left(P\left(X\leq Y_1\right)\leq u-y_2\right)\cdot\left(P\left(X\leq Y_2\right)\leq y_2\right)\cdot dy_2$$ But I still cannot figure out anything...

Upon a request, I'm uploading a picture of the question here:

Is there anything in the context of the problem making $Y_1$ and $Y_2$ continuous random variables? Or their cdf $F$ a continuous function? — kimchi lover, Apr 01 '21 at 17:20
@kimchilover Unfortunately, there is no such information given — DeBARtha, Apr 01 '21 at 18:05
@kimchilover Actually, this question was given in one of my class assignments a long time back and I had submitted it already (of course I couldn't do this problem). I can upload the screenshot of the question. — DeBARtha, Apr 01 '21 at 18:12
With this continuity assumption your problem is trivially covered by the "Probability integral transform ; without it, your problem is not solvable with the given data. — kimchi lover, Apr 01 '21 at 18:17
@kimchilover can you please formulate some hints and write them down in the answer? I couldn't do it properly — DeBARtha, Apr 01 '21 at 18:30
@DebarthaPaul: it seems that what you have is the sum of two independent uniformly distributed random variables in $(0,1)$; the resulting distrubution is the tent distribution over $(0,2)$ — Mittens, Apr 01 '21 at 18:34

score 2 · Accepted Answer · answered Apr 01 '21 at 18:37

It your random variables are continuous random variables then the Probability integral transform kicks in. The result is, if $X$ is continuous, then the random variable $Z=F(X)$, where $F$ is the distribution function for $X$, is uniformly distributed on $[0,1]$.

If your $Y_1$ and $Y_2$ are continuous, the distribution of your $U$ is the that of the sum of two independent $U[0,1]$ random variables, as Oliver Diaz guessed in a comment.

If your $Y_i$ are not continuous, that is, if there exists a number $a$ such that $P(Y_1=a)>0$, then the above answer is wrong, and the correct answer depends on details of the distribution of the $Y_i$.

Mittens · Answer 2 · 2021-04-01T19:15:23.013

1

Let $V:=F(Y)$, where $F$ is the distribution of $Y$. Then $V$ is a random variable taking values in $(0,1)$. For simplicity, assuming that $F$ is strictly monotone and continuous

$P[V\leq v]=P[F(Y)\leq v]=P[Y\leq F^{-1}(v)]=F(F^{-1}(v))=v$

For more general distriutions, you may use the quantile function $Q(q):=\inf\{x:F(x)\geq q\}$ which works like an inverse for $F$.

edited Apr 01 '21 at 19:15

answered Apr 01 '21 at 18:48

Mittens

39,145

Density Function of $F\left(Y_1\right)+F\left(Y_2\right)$

2 Answers2

Linked