0

This is a variant of a popular problem. In this variant, we sample the first point at which we cut a stick of length 1 uniformly from $U(0,1)$. The second cutting point is defined to be on the longer of the 2 segments after the first cut. We want to find the probability that the 3 segments form a valid triangle.

Let $X$ denote the first cut. Let $A$ denote the event that we form a valid triangle. Then $$ P(A) = P(A|X \leq 0.5) p(X \leq 0.5) + P(A|X > 0.5) p(X > 0.5) \\ = 2P(A|X \leq 0.5) p(X \leq 0.5) \\ = P(A|X \leq 0.5) $$

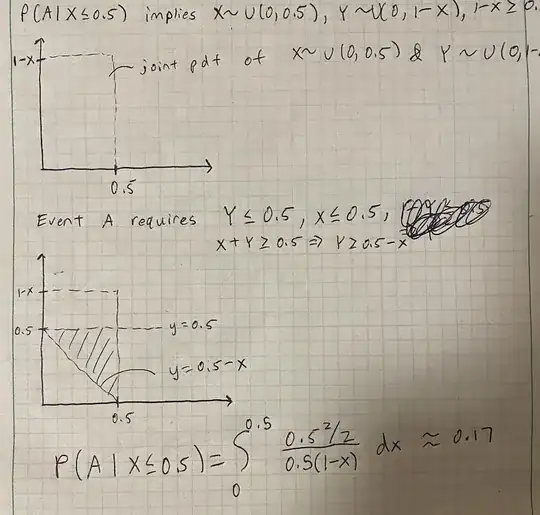
So I need to determine this conditional probability. When $X \leq 0.5$, we know the second cut $y$ can be sampled from $U(0, 1-x)$. So we consider the rectangular region bounded by $0 \leq x \leq 0.5$ and $0 \leq y \leq 1-x$ and note that $1 - x \geq 0.5$. This region defines the joint pdf of $X \sim U(0, 0.5)$ and $Y \sim U(0, 1-X)$.

The constraints that allow us to form a valid triangle within this rectangular region are $Y \leq 0.5$, $X + Y \geq 0.5$. These constraints create the shaded triangle in the picture below.

So I believe the answer should just integrate the area of the triangle divided by the area of the rectangular from $x = 0$ to $x = 0.5$. This gives approximately 0.17, which is not correct.

Here's a picture showing my work.

enter image description here

user5965026
  • 677

1 Answers1

1

I would do it this way . . .

Let $x$ be the length of the left piece from the first cut, and let $a=\min(x,1-x)$.

Let $b,c$ be the lengths from the next cut.

We want to find the probability that the lengths $a,b,c$ qualify as the side lengths of a triangle.

We can assume $a,b,c > 0$ and $a,b,c\ne {\large{\frac{1}{2}}}$ since those scenarios have zero probability.

Since $a+b+c=1$, it follows the lengths $a,b,c$ qualify as the side lengths of a triangle if and only if $0 < a,b,c < {\large{\frac{1}{2}}}$.

We already have $0 < a < {\large{\frac{1}{2}}}$, hence \begin{align*} & 0 < a,b,c < \frac{1}{2} \\[4pt] \iff\;& 0 < b,c < \frac{1}{2} \\[4pt] \iff\;& 0 < b,1-a-b < \frac{1}{2} \\[4pt] \iff\;& \frac{1}{2}-a < b < \frac{1}{2} \\[4pt] \end{align*} Note that for each $a$ with $0 < a < {\large{\frac{1}{2}}}$, the variable $b$ is uniformly distributed in the interval $(0,1-a)$.

Then since $$ \Bigl({\small{\frac{1}{2}}}\Bigr)-\Bigl({\small{\frac{1}{2}}}-a\Bigr)=a $$ it follows that for each fixed $a$ with $0 < a < {\large{\frac{1}{2}}}$, we have $$ P\Bigl(\frac{1}{2}-a < b < \frac{1}{2}\Bigr) = \frac{a}{1-a} $$ hence the probability that the lengths $a,b,c$ qualify as the side lengths of a triangle is equal to \begin{align*} & \int_0^{\frac{1}{2}} \frac{a}{1-a}\,dx + \int_{\frac{1}{2}}^1 \frac{a}{1-a}\,dx \\[4pt] =\; & \int_0^{\frac{1}{2}} \frac{x}{1-x}\,dx + \int_{\frac{1}{2}}^1 \frac{1-x}{x}\,dx \\[4pt] =\; & 2\int_0^{\frac{1}{2}} \frac{x}{1-x}\,dx \\[4pt] =\; & -1+2\ln(2)\approx .386294361 \\[4pt] \end{align*}

quasi
  • 58,772
  • I will study this in more detail in a little bit when I'm back on my computer. Do you know what was wrong with my thought process in my approach? – user5965026 Mar 31 '21 at 22:33
  • I don't see why you're using the area of the triangle as the numerator of your integrand. My solution is along the same lines as yours up to that point. – quasi Mar 31 '21 at 22:35
  • The triangle I was taking as the numerator of the integrand is not the area of the triangle that we're attempting to form, but the area of the triangle formed by the constraints. Are we referring to the same triangle? – user5965026 Mar 31 '21 at 22:38
  • I understand that, but I don't see how the area of that triangular region makes sense for the numerator of your integrand. – quasi Mar 31 '21 at 22:41
  • I must be misunderstanding something crucial here. I just included a picture of my work in the OP. Essentially, I thought that when we condition on $X \leq 0.5$, our sample space reduces to the rectangular region shown in the OP. And then we specify the constraints that form a valid triangle (event $A$), which forms that shaded rectangular region. So, isn't the pdf of the event conditioned on $X \leq 0.5$ just the area of the triangle divided by the area of the rectangle? – user5965026 Mar 31 '21 at 23:03
  • 1
    No, for each $x$ with $0 < x < {\large{\frac{1}{2}}}$, $y$ is uniformly distributed in the interval $(0,1-x)$ and of those possible values of $y$, the values that yield a triangle for the $3$ pieces are the values of $y$ such that $$ {\small{\frac{1}{2}}}-x < y < {\small{\frac{1}{2}}} $$ hence for each $x$, the fraction of qualifying $y$ values is $$ \frac{x}{1-x} $$ – quasi Mar 31 '21 at 23:24
  • 1
    Note also that in your formulation, if you correct the integrand to $$\frac{x}{1-x}$$ and then integrate for $x$ from $0$ to ${\large{\frac{1}{2}}}$, you would need to divide the result by ${\large{\frac{1}{2}}}$ to account for the conditional probability. – quasi Mar 31 '21 at 23:45
  • In regards to your last comment, are you implying that $\int_0^{0.5} \frac{x}{1-x} dx$ is $P(A, X \leq 0.5)$? – user5965026 Mar 31 '21 at 23:48
  • Also, as a minor note, the region bounded by the constraints $$ 0\le x\le \frac{1}{2}\ 0\le y\le 1-x $$ is trapezoidal, not rectangular. – quasi Mar 31 '21 at 23:50
  • Regarding your last query, after you integate, you still need to divide by ${\large{\frac{1}{2}}}$, or equivalently, multiply by $2$. – quasi Mar 31 '21 at 23:55
  • I'm now confused about my conditional probability approach... I understand your approach better – user5965026 Mar 31 '21 at 23:56
  • What is the name of the property for $\int_{0.5}^1 \frac{1 - x}{x} = \int_0^{0.5} \frac{x}{1-x}$? I recall there's a name for it from my calculus days but I can't remember what it was. – user5965026 Apr 01 '21 at 00:06
  • Just substitute $1-x=u$ in the integral on the left. – quasi Apr 01 '21 at 00:06
  • Wasn't there a special name for this case where you take the reciprocal of the integrand and offset the limits by a constant amount? I could be imagining this :) – user5965026 Apr 01 '21 at 00:07
  • In the case at hand, it's just a simple substitution. – quasi Apr 01 '21 at 00:09
  • The probability of $P(A, x \leq 0.5)$ is $0.386 / 2$, right? – user5965026 Apr 01 '21 at 00:44
  • When using your formulation, to understand why you would need to divide by ${\large{\frac{1}{2}}}$ at the end, note that $$ \int_0^{{\large{\frac{1}{2}}}}\frac{x}{1-x},dx $$ represents $$ P\Bigl(A,{\Large{\land}},\bigl(x < {\small{\frac{1}{2}}}\bigr)\Bigr) $$ – quasi Apr 01 '21 at 00:45
  • hence $$ P\Bigl(A,{\Large{\mid}},\bigl(x < {\small{\frac{1}{2}}}\bigr)\Bigr) = \frac { P\Bigl(A,{\Large{\land}},\bigl(x < {\small{\frac{1}{2}}}\bigr)\Bigr) } { P\bigl(x < {\small{\frac{1}{2}}}\bigr) } = \frac { {\displaystyle{ \int_0^{{\large{\frac{1}{2}}}}\frac{x}{1-x},dx }} } { \Bigl(\frac{1}{2}\Bigr) } = 2\int_0^{{\large{\frac{1}{2}}}}\frac{x}{1-x},dx $$ – quasi Apr 01 '21 at 00:45
  • Yeah I just realized that earlier, but when I draw the picture for the event $A \land (x < 0.5)$, I am seeing the probability is 0.125. I'm considering the region bounded by $x,y < 0.5$ and $y > 0.5 - x$, and the area appears to be 0.125. – user5965026 Apr 01 '21 at 00:47
  • https://imgur.com/a/tP08ylL. Here's the picture I mentioned. Am I drawing $A \land (x < 0.5)$ incorrectly? – user5965026 Apr 01 '21 at 00:53
  • 1
    The variable $x$ is uniformly distributed in the interval $$ \Bigl[0,{\small{\frac{1}{2}}}\Bigr] $$ and for each fixed $x$, the variable $y$ is uniformly distributed in the interval $$ \Bigl[ 0 , 1-x \Bigr] $$ but the points $(x,y)$ are not uniformly distributed in the trapezoidal region defined by the constraints $$ 0\le x\le\frac{1}{2}\ 0\le y\le 1-x $$ hence the ratio of the areas of the trianglular and trapezoidal regions is not relevant. – quasi Apr 01 '21 at 01:19
  • I think the "are not uniformly distributed in the trapezoidal region" is what I failed to understand. But why is it not uniformly distributed in that region? – user5965026 Apr 01 '21 at 01:26
  • Let us continue this discussion in chat. – quasi Apr 01 '21 at 01:41