4

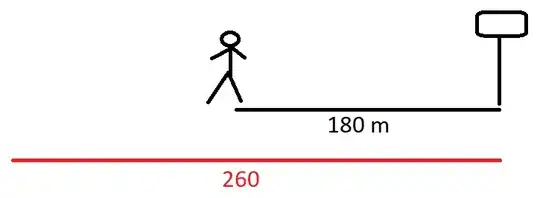
If I have a word problem with a fraction, how should I know which value should be in the numerator? Say I have the following problem:

"You stand 180 meters away from a radio tower. One wavelength is 260 meters. How many wavelengths away from the radio tower are you?"

My picture: enter image description here

I thought of this as an equation which I have to "balance", i.e. \begin{align} 180x &= 260 \\ x&= \frac{260}{180}= 1.45 \tag 1 \end{align} ... but this was wrong. In the correct answer, the numerator and denominator are flipped, i.e. \begin{align} x&= \frac{180}{260}= 0.69 \tag 2 \end{align}

How should I know which value should be in numerator? How should I think?

Update:

Great answers!

My confusion arised beacuse $\frac{180}{260}$ was correct instead of $\frac{260}{180}$. So suppose the question is instead formulated as:

"You stand 260 meters away from a radio tower. One wavelength is 180 meters. How many wavelengths away from the radio tower are you?"

enter image description here

But in this case I assume $x=\frac{180}{260}$ is wrong, and the correct answer is instead: \begin{align} 180x &= 260 \\ x&= \frac{260}{180}= 1.45 \tag 3 \end{align}

I.e. here $\frac{260}{180}$ is correct but in the first formulation $\frac{180}{260}$ was correct. How should I think so I not confuse the numerator/denominator in different cases?

Joyat
  • 127
  • 3
  • 1
    If 260 is one wavelength, how can you be more than one when you don't even stand one of those away? – Moo Mar 30 '21 at 16:01
  • 1
    "How should I know which value should be in numerator? How should I think?" Always look at the bigger picture. along the lines like @Moo told. For example, if you were to divide a pizza among 8 people equally, the bigger picture is how much each individual is getting. You have to make that that equal value the variable. So you would be having 8 times that equal value (the variable) equal to one pizza. – Adil Mohammed Mar 30 '21 at 16:05
  • Similiarly the variable here is the number of the wavelengths required to reach you, not not the number of times you have to move back so your distance from the radio is one wave way (think about the pizza example, if you invert the variable you will be getting how much pizza 8 people can eat, which is one pizza and which is not an useful info) – Adil Mohammed Mar 30 '21 at 16:08
  • 1
    Try answering the question when 180 and 260 are replaced with "simpler to intuit" numbers, such as 1 and 2, or 2 and 4, or 1 and 3, or 3 and 9, etc. – Dave L. Renfro Mar 30 '21 at 16:12
  • I have updated my post with a hint to your newly added question. – DeBARtha Mar 31 '21 at 11:19

3 Answers3

3

Note the question carefully:

"How many wavelengths away from the radio tower are you?"

Clearly, it wants you to find out the number of wavelengths. Now you may proceed as:

Suppose the number of wavelengths is $x$.

Can you take it up from here?

Then the length of $x$ wavelengths in all is $260x$. Thus, to cover $180$m, we should have $$260x=180\implies x=\frac{180}{260}=\frac{9}{13}\approx0.69$$

Update: Now for the question which you added later...

Similar logic here also. The length of a wavelength is $180$m. Say the number of wavelengths required to cover $260$m is $y$.

Then think what the total length of all the $y$ wavelengths taken together will be and equate it with your distance from the tower.

The total length of all the $y$ wavelengths taken together is $180y$.

Thus, to cover $260$m, the number of wavelengths required will be $$180y=260\implies y=\frac{260}{180}=\frac{13}{9}\approx1.44$$

DeBARtha
  • 609
2

This is known as a problem in dimensional analysis.

$$180 ~\text{meters} \times \frac{1 ~\text{wavelength}}{\text{260 meters}} ~=~ \frac{180}{260} ~\text{wavelengths}.$$

To illustrate with a more familiar example, suppose that you drive for $(2)$ hours, at a speed of $(60)$ miles per hour. How far have you driven?

$$2 ~\text{hours} \times \frac{60 ~\text{miles}}{\text{1 hour}} ~=~ (2 \times 60) ~\text{miles}.$$

user2661923
  • 35,619
  • 3
  • 17
  • 39
2

It's possible that a certain amount of confusion with fractions arises because the terms "numerator" and "denominator" aren't commonly used in other contexts. In a fraction $\frac{p}{q}$:

  • The denominator $q$ specifies "how many things" make one unit, i.e., it denominates the value of $\frac{1}{q}$.

  • The numerator $p$ specifies "how many units" $\frac{1}{q}$ there are in the fraction, i.e., it counts or enumerates portions of size $\frac{1}{q}$.

Here, the "unit of stuff" is one wavelength. There are $q = 260$ meters in one wavelength, so one meter is $\frac{1}{260}$ wavelengths. If we want to know what fraction of a wavelength is $180$ meters, we take $180$ one-meter units, so $p = 180$, hence $\frac{p}{q} = \frac{180}{260}$ wavelengths.

Andrew D. Hwang
  • 78,195