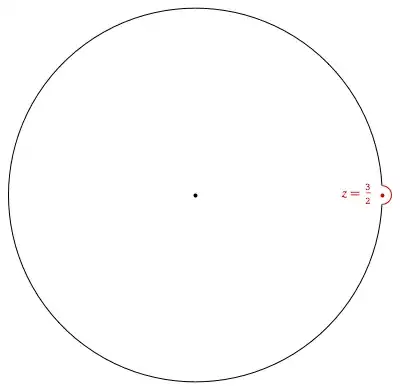
Been struggling a while to solve the following integral:
$$\int_C\frac{ze^z}{2z-3}$$ where C is $$|z| = 1.5$$.
I found a very similar case here but it's outside of what we learned in class. Covered Cauchy's Integral Theorem but not residue theorem yet.
I know that we cannot use the Cauchy Integral Formula $$f(z_0) = \frac{1}{2\pi i}\int_C \frac{f(z)}{z-z_0}dz$$ since $z_0$ needs to be inside the contour.
Can someone please give me a hint as to how to solve this integral? Thank you in advance!
As it stands, the integral does not converge in the standard sense. This is because if we remove a small region around the singularity, the value of the integral depends greatly on how that region shrinks to $0$.
However, using the Cauchy Principal Value, we can get a value.
Avoid the singularity with a small bump around it:
The contour integral is $$ \int_{C\text{ with bump}}\frac{ze^z}{2z-3}\,\mathrm{d}z=\frac32\pi ie^{3/2} $$ However, the Cauchy Principal value is the integral along the black circle minus an infinitesimal symmetric interval around the singulrity, so we subtract off the contribution from the red bump, which is $\frac34\pi ie^{3/2}$, since the bump is half a circle (counter-clockwise) and the singularity is first order.
Therefore, $$ \mathrm{PV}\int_C\frac{ze^z}{2z-3}\,\mathrm{d}z=\frac34\pi ie^{3/2} $$
