3

I was playing around with desmos, when i saw this

enter image description here

I think that:

  • $\sin(\sin(\sin(\cdots)))$ will approach zero veeeery slowly, also approaching a square wave.

  • $\cos(\cos(\cos(\cdots)))$ will approach $0.7389$.

  • $\sin(\cos(\sin(\cos(\cdots))))$ will approach $0.948$.

Are these hypothesis correct? Is there any formal proof?

Blue
  • 75,673
gdor11
  • 173

2 Answers2

7

By the fixed-point theorem, when an iteration like

$$x_{n+1}=f(x_n)$$ converges, it converges to a solution of $f(x)=x$.

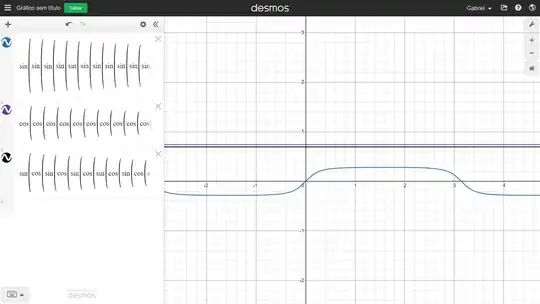
Here is a plot of your $f$'s, which confirm the values you found:

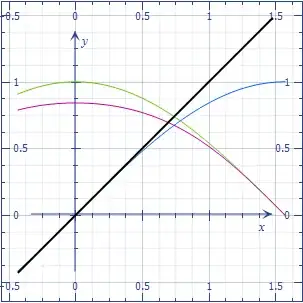
enter image description here

A convergence criterion is $|f'(x)|<1$, which is achieved by your last two functions. Convergence is linear (the number of exact digits grows proportionally to the $n$).

The case of the sine is a little more difficult. But as $|\sin(x)|<|x|$, convergence to $0$ is guaranteed.

If we assume $\sin^{(n)}(x)\sim cn^\alpha$, we have

$$\sin^{(n+1)}(x)=\sin^{(n)}(x)-\frac{(\sin^{(n)}(x))^3}6+o((\sin^{(n)}(x))^3)$$

corresponding to

$$c(n+1)^\alpha\sim cn^\alpha-\frac c6n^{3\alpha},$$ which gives $\alpha=-\frac12$ by identifying the second terms, and

$$\sin^{(n)}(x)\sim\frac c{\sqrt n}.$$

This convergence is extremely slow.

As you probably already figured out, the iterations of $\cos(\sin(\cos(\sin(\cdots))))$ will converge to the value of $\cos(x)$ where $x$ is the limit of $\sin(\cos(\sin(\cos(\cdots))))$.

  • is there any explanation of why sin(sin(sin... approaches c*|sin(x)|/sin(x) with c tending to zero? – gdor11 Mar 29 '21 at 14:35
  • @Gabriel: the sine being an odd function, the sign is preserved. –  Mar 29 '21 at 14:43
  • but why not something like c*sin(x)? or any other function that preserves sign and approaches zero? – gdor11 Mar 29 '21 at 14:49
  • 1
    @Gabriel: as you can check, the derivative of the iterated functions become smaller and smaller, giving a flatter and flatter curve. (Anyway, the derivative remains $1$ at $x=0$.) –  Mar 29 '21 at 15:05
  • pages 153-166 in de Bruijn, Asymptotic Methods in Analysis . Formula 8.8.8 on page 166 says $ \frac{\sqrt 3}{\sqrt n}. $ I see, the second error term refers to a solution of the Abel equation (8.74) on page 160, $\psi( \sin x) - \sin x = 1 $ – Will Jagy Mar 29 '21 at 17:25
0

For the iterated sine you can use the following: Since $|\sin(x)|\leqslant 1$ you can deduce that $\sin(\sin(x))\in[-\sin(1),\sin(1)]$ and you can easily see that $\sin(1)<1$ using Taylor expansion. Now if you take a sequence given by $\varepsilon_n = \sin(\varepsilon_{n-1})$ with say $0<\varepsilon_0<1$, then you get (since for all $0<x<1$ you have $0<\sin(x)<x$) a decreasing sequence $\varepsilon_n$ which is bounded below by $0$. Then you know that your sequence converges: In the limit you will have $\sin(\varepsilon_\infty)=\varepsilon_\infty$ and hence $\varepsilon_\infty=0$.

frog
  • 2,381