$X_1 ,X_2 $ are two sample from a unknown distribution with CDF $F$ such that sample range and minimum order statistics are independent. Show that $F$ must be cdf of exponential distribution.
I wrote the joint pdf of range and minimum order statistics but cant proceed further that is if range${}=R$ and min order statistics is $S$ then $f(R+S)f(s)=f(R)f(S)/2$ but cant proceed further help!
Not a full answer but is too long for comments. The challenge for me in the second part arises because I have made no assumptions about the support of $X$. Does the problem statement make any mention about $\operatorname{supp}(X)$?
We have $X_1,X_2\overset{\text{i.i.d.}}{\sim}F_X$ with $\operatorname{supp}(X)=(a,b)$. Using the standard derivation one has for the joint distribution of the order statistics $$ f_{X_{(1)}X_{(2)}}(x_1,x_2)=2f_X(x_1)f_X(x_2),\quad a<x_1<x_2<b. $$ Let, $(M,R)=(X_{(1)},X_{(2)}-X_{(1)})$. It follows that the inverse transformation and Jacobian is $(X_{(1)},X_{(2)})=(M,M+R)$ and $|J|=1$, respectively. We then have $$ f_{MR}(m,r)=2f_X(m)f_X(r+m),\quad (r,m)\in D, $$ where $D$ is as seen in the folowing image.
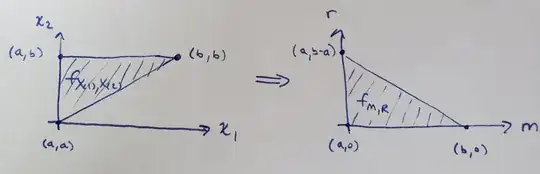
Part 1: $X_1,X_2\overset{\text{i.i.d.}}{\sim}\operatorname{Exp}(\lambda)\implies M\perp R$:
If $X_1,X_2\overset{\text{i.i.d.}}{\sim}\operatorname{Exp}(\lambda)$ then $a=0$, $b=\infty$, and $D=(0,\infty)\times (0,\infty)$ so that $$ f_{MR}(m,r)=2\lambda e^{-\lambda m}\lambda e^{-\lambda(r+m)}=\underbrace{2\lambda e^{-2\lambda m}}_{f_M(m)}\underbrace{\lambda e^{-\lambda r}}_{f_R(r)},\quad (m,r)\in(0,\infty)^2, $$ which shows that $M\sim\operatorname{Exp}(2\lambda)$, $R\sim\operatorname{Exp}(\lambda)$, and $M\perp R$.
Part 2: $M\perp R\implies X_1,X_2\overset{\text{i.i.d.}}{\sim}\operatorname{Exp}(\lambda)$:
