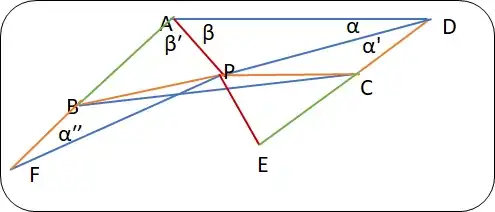
Given a quadrilateral $ABCD$, where $|AD|=|AB|+|CD|$ the angle bisectors of $BAD$ and $ADC$ intersect at $P$. The task is to prove that $|BP|=|CP|$.
Since $|AD|=|AB|+|CD|$, the quadrilateral cannot be tangential, and thus the intersection points of adjacent angle bisectors are not concurrent and instead they form the vertices of a cyclic quadrilateral. This seems like an important piece of information, but I haven't been able to get any further.
Thank you for your help.