2

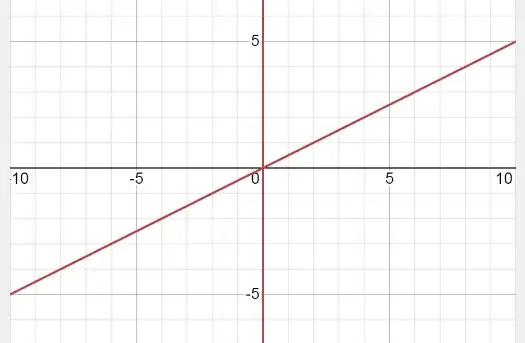
Suppose I am given the equation $x=2y$.

My interpretation of this equation is $A=\{\langle x,y \rangle \in \mathbb R \times \mathbb R |\ x=2y\ \}$

Given this interpretation, I want to know the difference between the equations $x^2=4y^2$ and $x^2=2yx$.

For the equation $x^2=2yx$, we have a single line that completely overlaps with $x=2y$.

For the equation $x^2=4y^2$, we have two intersecting lines, only one of which overlaps with $x=2y$.

In either case, this is satisfying because it explains the logical concepts of:

$$x=2y \implies x^2=4y^2$$ $$\text{and}$$ $$x=2y \implies x^2=2yx$$ which I feel as though I am implicitly using during different algebraic proofs. That is to say, the set of solutions for $x=2y$ also satisfies (intersects with) the equations (sets) $x^2=4y^2$ and $x^2=2yx$.

In line with our earlier set interpretation, letting $x^2=2yx$ represent the set $B=\{\langle x,y \rangle \in \mathbb R \times \mathbb R | x^2=2yx\}$ and letting $x^2=4y^2$ represent the set $C=\{\langle x,y \rangle \in \mathbb R \times \mathbb R | x^2=4y^2\}$, the aforementioned implication suggests $A \subseteq B$ and $A\subseteq C$.

However, given my descriptions of the graphs, it is quite clear that we can be more specific...namely:

$A=B$ and $A \subsetneqq C$

I see that for the equation $x^2=4y^2$, square rooting both sides yields $\pm x=2y$, which explains its graph of the two intersecting lines. But I am wondering if there is a more fundamental reason that explains this observation. In particular, the quality of inverse exponents versus the quality of inverse multiplication.

To simplify $x^2=2yx$, I am effectively multiplying each side by $x^{-1}$. Comparatively, to simplify $x^2=4y^2$ (perhaps better written as $x^2=(2y)^2$), I am taking the inverse operation of squaring. It seems like the inverse operation of squaring yields "more solutions" than the inverse operation of multiplication.

Any added insight would be greatly appreciated!

S.C.
  • 4,984
  • 5
    if x is zero in the second equation then y can assume any value – MIO Mar 27 '21 at 17:39
  • @aldodecristo good point. So each equation produces two intersecting lines, right? (albeit, different intersecting lines) – S.C. Mar 27 '21 at 17:41
  • 2
    well no in the first equation you just get a line. In the second one you also have the $y$ axis. The first equation isn't satisfied by $x=0, y=1$ but the second one does – MIO Mar 27 '21 at 17:43
  • 2
    $x^2=4y^2$ is equivalent to $(x-2y)(x+2y)=0$, so that either $x-2y=0$ or $x+2y=0$; the solution set is the union of two lines. Likewise, $x^2=2yx$ is equivalent to $x(x-2y)=0$, so that either $x=0$ or $x-2y=0$; again, the solution set is the union of two lines. – Blue Mar 27 '21 at 17:44
  • @Blue For clarification then, it seems as though when you go from $x^2=4y^2$ to its equivalent form $(x-2y)(x+2y)=0$, you haven't added any solutions. However, when you go from $x=2y$ to $x^2=4y^2$, you do add solutions. Does that mean the word "equivalence" is really reserved for expressions that do not change the solution set (i.e. it would be wrong to say that " $x=2y$ is equivalent to $x^2=4y^2$")? – S.C. Mar 27 '21 at 17:51
  • @S.Cramer: To quote from Lewis Carroll's Through the Looking Glass: "When I use a word," Humpty Dumpty said, in rather a scornful tone, "it means just what I choose it to mean—neither more nor less." :) ... That said, I suspect you'd be pretty hard-pressed to find many who'd consider "equivalent" the best way to describe $x=2y$ and $x^2=4y^2$ without any context. – Blue Mar 27 '21 at 18:04

4 Answers4

3

It is easier to compare if you set $0$ alone on one side.

Your first equation is $x-2y=0$. The two next equations are $x^2-4y^2=0$ and $x^2-2xy=0$. So what to do with those equations? Factor them!

We have $x^2-4y^2=(x-2y)(x+2y)=0$. Since a product is zero iff one of the factors is zero, this equation describes the union of two lines: $x-2y=0$ and $x+2y=0$.

We have $x^2-2xy=x(x-2y)=0$. Since a product is zero iff one of the factors is zero, this equation describes the union of two lines: $x-2y=0$ and $x=0$.

At least to me, things become a lot clearer if we have $0$ on one side of the equation, and factor. These two actions work very nice together in order to couple what's going on with the algebra with what's going on with the geometry. It is not always this easy to factor, but the principle remains.

Arthur
  • 199,419
  • Awesome. Thank you. One lingering question I have though: When we "rearrange an equation" as you did through factoring and addition(subtraction), you didn't change the solution set. i.e. the set of ordered pairs that satisfy $x^2=4y^2$ are exactly the set of ordered pairs that satisfy $(x-2y)(x+2y)=0$. However, when I square $x=2y$ or when I multiply $x=2y$ by $x$, I DO change the solution set...i.e. the set of ordered pairs that satisfy $x=2y$ is not the same as the set of ordered pairs that satisfy $x^2=4y^2$ or $x^2=2yx$. Why exactly is this? – S.C. Mar 27 '21 at 18:11
  • Why is "factoring + addition" so different from these other two formula manipulation strategies (squaring or multiplying by $x$). – S.C. Mar 27 '21 at 18:11
  • 1
    @S.Cramer Because factoring takes an expression and returns an expression with the exact same value. So I can do that to one side of an equation without changing its solution set. And adding a fixed term is an entirely reversible operation (a so-called injection: if I add 3 to whatever I have and end up with 8, you know exactly what I started with, and the same is true no matter what I add), so doing that to both sides does not in any way change when they are equal. – Arthur Mar 27 '21 at 18:24
  • 1
    Squaring is not an injection (if I square something and end up with $25$, you don't know exactly what I started with), so doing that to both sides of an equation gives you extra solution. As for multiplying with $x$, that's an injection as long as we stay away from the region where $x$ is $0$ (the $y$-axis). This is reflected in the fact that outside of that region, $x-2y = 0\to x^2-2xy = 0$ changes nothing about the solution set. Within that region, though, it collapses everything to $0$ and the entire axis becomes part of the solution set. – Arthur Mar 27 '21 at 18:24
  • Ahhh. Perfect. Literally exactly what I was looking for. Cheers! – S.C. Mar 27 '21 at 18:27
  • (So basically, for any operation that has a group structure, the solution set will not change, right?) ...The group structure for the multiplication operation has no inverse at the zeroth element and therefore we run into the problem that you described. – S.C. Mar 27 '21 at 18:31
  • 1
    @S.Cramer I like the notion of injection and reversibility, personally, rather than groups. But yes, it goes along those lines, yes. – Arthur Mar 27 '21 at 18:57
2

$\displaystyle x^2=4y^2$

$\iff$ $\;y=\pm\frac12x$ enter image description here

$\displaystyle x^2=2yx$

$\iff$ $\;x=0\quad$ or $\quad y=\frac12x$ enter image description here

ryang
  • 38,879
  • 14
  • 81
  • 179
2

Well if $x= 2y$ then $x^2 =4y^2$ but $x^2=4y^2 \not \implies x = 2y$. (But it does imply $x = \pm 2y$).

So $A = \{(x,y)| x=2y\}\subsetneq \{(x,y)|x^2 =4y^2\}=B$. If we want to interpret these sets $A $ is a line and $B$ is two crossed lines; one of them is $A$ and the other is the mirror image of $A$.

And also $x=2y \implies x^2 = 2xy$ but $x^2 =2xy \not \implies x=2y$. (But it implies: If $x\ne 0$ then $x = 2y$. But if $x = 0$ then $y$ may be any value.)

So again $A = =\{(x,y)|x=2y\}\subsetneq \{(x,y)|x^2 =2xy\}=C$. If we want to interpret these sets $A$ is a line and $B$ is two crossed lines: one of them is $A$ and the other is the vertical line $x=0$.

As $A \subset B$ and $A \subset C$ then $A\subset B\cap C$. And in this case we have

If $x^2 = 4y^2=2xy$ then we have $x^2 = 4y^2 \implies x =\pm 2y$ and $x^2=2xy\implies x=0$ or $x = 2y$ we have $x=2y$ or $x=0=-2y$. So $x = 2y$.

So $B\cap C = A$ in this case.

....

SO that about covers is.

$x^2 =4y^2$ includes all of $x=2y$ but also adds $x = -2y$ solutions. $x^2 = 2xy$ includes all of $x = 2y$ but also adds $x =0;y=anything$.

So $x^2 = 4y^2$ and $x^2 = 2xy$ have $x =2y$ in common and $x=0=-2y$ in common. But $x=0=-2y$ is part of $x =2y$ so that only have $x=2y$ in common.

fleablood
  • 124,253
  • hmmm. When you write $x^2=4y^2 \not \implies x = 2y$, is it not true that $[P \rightarrow Q \land R] \rightarrow [ P \rightarrow Q]$ is a tautology? That is to say, because $x^2=4y^2 \rightarrow x=\pm 2y$, then necessarily $x^2=4y^2 \rightarrow x=2y$. (Sorry, not trying to be pedantic, just trying to make sure I follow the argument logically) – S.C. Mar 27 '21 at 20:36
  • 1
    Of course not. $x^2 = 4y^2$ implies $x = 2y$ *OR* $x=-2y$. That is completely different then $x=2y$ *AND* $x = -2y$. Although $[P\to(Q\text{ AND }R]\to [P \to Q]$ is a tautology, $[P\to(Q\text{ OR }R]\to [P \to Q]$ certainly is not. And $x^2= 4y^2 \to x=\pm 2y$ most certainly and obviously does not mean $x^2=4y^2\to x= 2y$. Just consider any case where $y\ne 0$ and $x = -2y$. For example $y=3$ and $x = -6$. Then we have $x^2 =(-6)^2=36=4(3^2)=4y^2$ but that does not* mean $-6=x = 2y = 6$. $-6 \ne 6$. – fleablood Mar 27 '21 at 23:22
  • 1
    You are the second person I've met who somehow was under the impression that $a = \pm 3$ seemed to mean that $a$ was somehow equal to both $3$ and $-3$ at the same time. That is not what $a=\pm 3$ means and such a statement would be utterly nonsensical and inconsistent. $-3$ and $3$ are different values and values can only equal one thing at a time. They can't equal two different things. .. What $a = \pm 3$ means is $x = 3$ OR $x = -3$ but we can't not or do not or don't care to distinguish which at this time. – fleablood Mar 27 '21 at 23:27
  • thank you for the comments! The english phrasing I used that led to the confusion is the sentence "the set of solutions to $x=2y$ and the set of solution to $x=-2y$ create the set of solutions for $x^2=4y^2$". I see now that because we use the union to describe the set, or is the appropriate connective. – S.C. Mar 28 '21 at 00:26
0

Suppose $$x = 2y \tag{1}\label{eq1}$$ Then certainly $$x^2 = 4y^2 \tag{2}\label{eq2}$$

Now, if all we know is $x^2 = 4y^2$, then we would know either $x = 2y$ or $x = -2y$. However, we know more than this. We can eliminate $x = -2y$ because of $\eqref{eq1}$.

$x = 2y$ doesn't stop being true even after squaring both sides. \eqref{eq2} implies two posibilies, one of which we can eliminate because of \eqref{eq1}.

(To be more precise, $x=-2y$ is eliminated for $x, y \neq 0$. The solution $x = y = 0$ is fine, and is already covered by $x = 2y$.)

Ben
  • 1,585