4

I am trying to find the odds of getting the letters I need. We start with 2 groups

A B C D      A B C D
E F G H      E F G H

The group is random so its not always A..H in that order When you use a letter its taken out of the group.

I can only take letters out that are in the first 4 (or top row) in the group. So if I took "C" then one letter from the 2nd row moves up into the "C" Positon.

May look like this

A B G D    A B E D
E F H      F G H

where a random letter is moved up , not always the same but can be in each group.

My question is Whats the odds of both players being able to take A, B, C, D, E in that order from the top row with out skipping a turn.

Not sure what Tag to add if you know please let me know and ill add it. Thanks

glen morse
  • 41

1 Answers1

2

HINT:

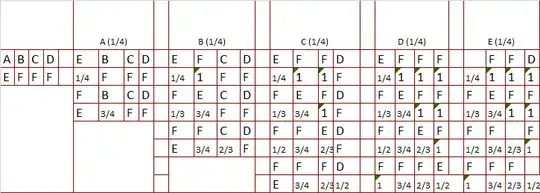
Here is a demonstration of a simpler configuration: we begin with the pattern ABCD on top rows and EFGH on bottom rows. In this case, The approach is straightforward, but tracing takes some patience. Hope this provides some insight.

Let P(A) and P(B) represent the probabilities of each one of two players being able to take A, B, C, D, E in that order. The probability for both to be successful is P(A)$\cdot $P(B), where P(A)=P(B).

In this picture , F,G,H can be treated the same, we can use F,F, F to simplify the picture. Every time you draw from top row, you only have $\frac{1}{4}$ chance to be correct. Pay attention to separate move ups of E and F as illustrated.

For example, for 1st step to take A out from first row , the probability is $\frac{1}{4}$.When you move a letter up to fill A's position from second row, the probability for E is $\frac{1}{4}$ , while for F is $\frac{3}{4}$ . With some analysis, it is concluded there are three paths leading to a successful game. For each path, trace the success possibilities for every step and multiply them, we get the success rate for that path.

Adding everything together:

$P(A)=P(B)=(\frac{1}{4})^6+\frac{1}{4}\frac{3}{4}\frac{1}{4}\frac{1}{3}\frac{1}{4}\frac{1}{2}\frac{1}{4}\frac{1}{1}\frac{1}{4}+\frac{1}{4}\frac{3}{4}\frac{1}{4}\frac{2}{3}\frac{1}{4}\frac{1}{2}\frac{1}{4}\frac{1}{1}\frac{1}{4}=(\frac{1}{4})^6(1+\frac{1}{2}+1)$

$P(A)P(B)=(\frac{1}{4})^{12}(\frac{5}{2})^2=25\cdot (\frac{1}{4})^{13}\approx 3.7252902985×10^{−7}$

What a chance!

enter image description here

Star Bright
  • 2,338
  • Looks good. 3% seems low though. Does this consider if you start with A and B in top row. Then round 2 is 100% cause B was there all ready? It seems you did. But still seems low lol – glen morse Mar 27 '21 at 16:55
  • This assmes ABCD top row, EFFF bottom row to begin with. The probability is 0.4 x 10^{-7}, not 3%. But now, I realize your problem starts with random pattern, then it is a different and more difficult one, I guess the probability will be even lower. I will leave my answer as a reference only. I will think about it given time. – Star Bright Mar 27 '21 at 18:39