Consider $C([a,b])$, the vector space of continuous functions in $[a,b] \subset \mathbb{R}$ to $\mathbb{R}$. Let be $f \in C([a,b])$, we define $\|\cdot\|_1$ as follows: \begin{equation*} \|f\|_1 = \int_{a}^{b}|f(x)|dx \end{equation*}
I must show that $(C([a,b]), \|\cdot\|_1)$ is not a Banach space.
This is my answer the which one is wrong according to my teacher. Consider the following counterexample. Let $c =2^{-1}(a+b)$ y $f_n:[a,b] \rightarrow \mathbb{R} \hspace{.1cm} \forall n \in \mathbb{N}$ with the following association rule and graph:
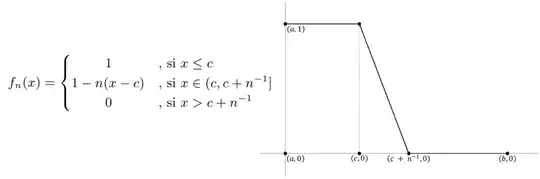
It's clear that $\{f_n\}_{n \in \mathbb{N}} \subset C([a,b])$. We will show that $\{f_n\}_{n \in \mathbb{N}}$ it's a $||\cdot||_1-Cauchy$ sequence. Let be $\epsilon > 0$ and $N = \displaystyle \left\lceil{ \frac{1}{2 \epsilon}}\right\rceil$, then: \begin{equation*} ||f_n-f_m||_1 = \int_{a}^{b} |f_n(x)-f_m(x)|dx = \left| \frac{1}{2n}-\frac{1}{2m} \right| \leq \max \left\{ \frac{1}{2n}, \frac{1}{2m}\right\} < \epsilon, \hspace{.1cm} \forall n,m \geq N \end{equation*} So the sequence is $||\cdot||_1-Cauchy$, however though this sequence converges to the following limit function, the limit function is clearly discontinuous. Let be $f:[a,b] \rightarrow \mathbb{R}$: \begin{equation*} f(x) = \begin{cases} 1 & \text{si $x \leq c$}\\ 0 & \text{si $x > c$} \end{cases} \end{equation*} Fixed $\epsilon_1 > 0$ and $N_1 = \left\lceil{\displaystyle\frac{1}{2 \epsilon_1}}\right\rceil$, then: \begin{equation*} ||f_n-f||_1 = \displaystyle\int_{0}^{1} |f_n(x)-f(x)| = \frac{1}{2n} < \epsilon, \hspace{.1cm} \forall n \geq N_1 \end{equation*} $\textbf{Now, the problem is that}$ (according to my teacher) I only have propose a discontinuous function wich is a limit of the sequence, this does not means that do not exits another continuous function wich is also the limit of the sequence. I understand the problem, but nothing comes up to me to solve this.