1

In the making of a pen case for expensive fountain pens, I affix equally-spaced wooden half-rounds to the bottom inside surface of, say, a cigar box and cover the surface with felt. The half-rounds and felt prevent the pens from rubbing up against each other. When completed, the case is a good way to display the pens when the hinged top is open, as well as to keep dust out when the hinged top is closed. Jewelers might do something similar in a section of a glass-enclosed display case to display longer items such as bracelets, necklaces, and more.

One obvious way of measuring a piece of felt that will cover completely the hills and valleys of the surface, when cut, is to take a longer-than-needed piece of felt of the correct width, cover the "lands and grooves" with it, and mark the place on the felt where it completely covers the surface. Then cut it and paste it (permanently) to the bottom of the box and to the half-rounds.

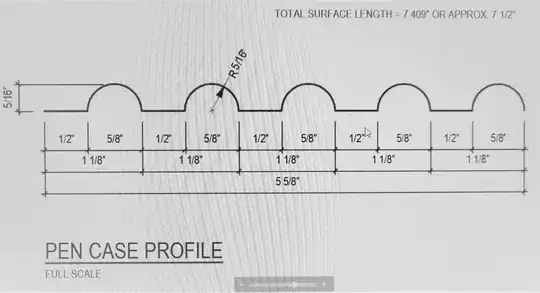
As an alternative, however, is there a way to measure the length of felt needed by using a formula for any size of box?

For example, if the bottom of the box is five inches from front to back; if the half rounds have a diameter of 5/8 of an inch; and if the spaces between the half-rounds are the same (say, half an inch, plus or minus); what would the formula be to measure and cut the piece of felt?

The only tag I could think of is "arc-length," as I am not a mathematician, as you can probably tell. By the way, I may in the near future add to this question a two-dimensional drawing of what I'm describing, for your ease in answering my question.

Thanks to an architect friend of mine:

enter image description here

Is there a formula in there somewhere?

rhetorician
  • 113
  • It seems like there could be a certain amount of stretch involved to fit the felt smoothly, unless the profile is uniform in one direction (i.e. if there is a direction on the work for which all cross-sections are straight lines). However all this means is that a mathematical treatment might produce dimensions that still involve some trimming, so you question stands. – Joffan Mar 25 '21 at 17:37

1 Answers1

1

If I understand the question correctly, it's pretty simple. If you have $n$ segments where each segment consists of a flat area of width $w$ followed by a semicircle of diameter $d$, then the total arc length is $$s = n(w + \pi d/2)$$

In the drawing we have $$\begin{align} n &= 5\\ w &= 1/2 \\ d &= 5/8 \end{align}$$ so $$s = 5 \times (0.50 + 3.14 \times 0.625 / 2) = 5 \times 1.481 = 7.41$$

awkward
  • 14,736