1

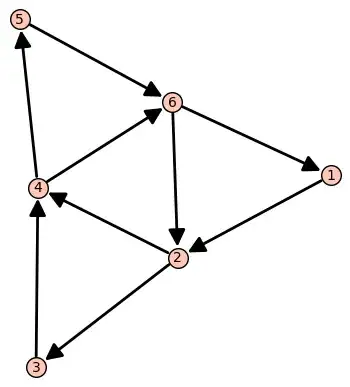
I am working with SageMath on graphs, in particular on this graph:

enter image description here

I have found that its automorphism group is generated by the elements $(1,3,5)$ and $(2,4,6)$: how do I find to which group is this group isomorphic to? I ask both computationally and mathematically.

Shaun
  • 44,997
mattiav27
  • 413
  • 3
    Something seems off about this. Ordinarily $(1,3,5)$ would stand for the permutation that takes $1$ to $3$, takes $3$ to $5$, takes $5$ to $1$, takes $2$ to itself, takes $4$ to itself, and takes $6$ to itself. Are you sure that this is an automorphism of the graph? – Lee Mosher Mar 25 '21 at 16:14
  • 3
    It loos to me as though the automorphism group is generated by the single permutation $(1,3,5)(2,4,6)$, so it is cyclic of order $3$. – Derek Holt Mar 25 '21 at 17:31

2 Answers2

0

The permutations $(135)$ and $(246)$ commute, so this automorphism group is just the direct product of the cyclic groups they generate, i.e. is isomorphic to $(\mathbb{Z}/3\mathbb{Z}) \times (\mathbb{Z}/3\mathbb{Z})$.

I don't know a computational way to recognize the isomorphism class of a group from realizing it as a subgroup of $S_n$ (that might even already be an undecidable problem, not sure). It is likely GAP or some such software can attack this problem, though.

hunter
  • 29,847
  • 1
    If it's a subgroup of $S_n$ then there are only finitely many choices and they can be enumerated; it's surely not efficient, but the problem must be decidable. – Steven Stadnicki Mar 25 '21 at 17:20
  • 2
    But what exactly does "Recognize the isomorphism class of a group" mean? You can compute a composition series of the group and identify the composition factors in polynomial time. – Derek Holt Mar 25 '21 at 17:28
  • (agree w both of you) – hunter Mar 25 '21 at 19:12
0

Since they are disjoint three-cycles, they commute and have order three; there are no other restrictions on the group; so the group is isomorphic to the group given by the presentation

$$\langle a,b\mid a^3, b^3, ab=ba\rangle,$$

which is $\Bbb Z_3\times\Bbb Z_3$.

Computationally, you could use GAP.

If the automorphism group is, instead, generated by $(135)(246)$, then it is cyclic and the order of the group is that of the generating element, which is three; hence it is isomorphic to $\Bbb Z_3$.

Shaun
  • 44,997