Introduction to Complex Analysis by H. A. Priestley (Revised ed.) shows a diagram (page 40) which is a polygonal path in a set $G$ (link below). Their proof claims we can polygonally pave our way from $z$ to $a$ by using the fact that open discs centred at $z$ enclose a point $w$ such that the line segment $[z,w]\subset D(z;r),r>0$. I am confident in that notion, but maybe it's their diagram which confuses me.
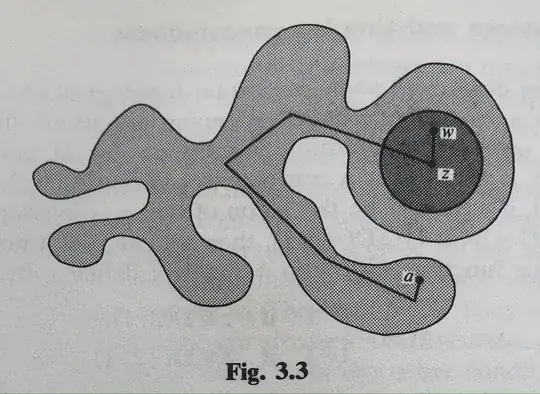
It displays large line segments paving through the set $G$ which if you were to draw open discs centred from the original point, the open disc is then not contained by $G$. I assume they could have used smaller open discs, therefore, more $w$s to get to $a$.
Any clarification on this topic would help me out a lot. Thank you very much.