0

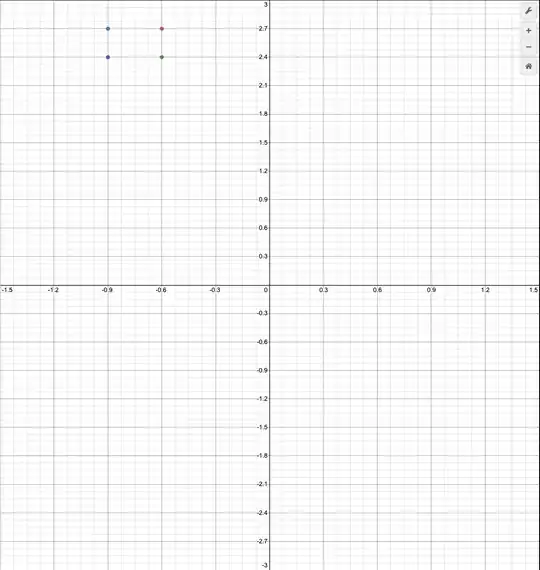
enter image description hereFor example, I have a grid where the x-axis goes from -1.5 to 1.5, with an interval of 0.3 (i.e. -1.5 would go to -1.2 then -0.9 and so on).

The y-axis goes from 3.0 to -3.0 with an interval of 0.3 as well.

How can I identify a unique square within this grid just by its vertices?

I tried to sum up the vertices which make up the square, but the sum of the vertices is not unique and can apply to a few other squares within the grid as well.

EDIT FOR CLARIFICATION:

Is there a way to use vertices like these to help me identify the square in the graph? I am designing a game where I want to be able to check if the box is currently occupied. I only have access to the vertices surrounding the box.

flutterbug98
  • 159

1 Answers1

1

You can find the center of a square by finding the mid-point of it's diagonal: $$(h,k) = \left( \frac {x_2+x_1} {2}, \frac {y_2+y_1} {2} \right)$$ Where $(h,k)$ represents the center. You can then get the side length by finding the distance between any two adjacent vertices: $$\text{side length (r)} = \sqrt{(x_2-x_1) + (y_2-y_1)}$$ And then you can use this formula to identify the square: $$\left|(x - h) + (y - k) \right|+\left| (x - h) - (y - k) \right|=r$$

Anas Khaled
  • 775
  • r would give me a unique number for each square? – flutterbug98 Mar 24 '21 at 03:53
  • $r$ is not the output, $r$ is one of the values that you need to define the square. The whole equation is the input, and the output is the square. You can use any graphing app to graph that equation, by substituting $h, k, r$ with the suitable values, you should see a square. And if you don't have those values, and you only have coordinates of vertices, I showed you how to derive them. – Anas Khaled Mar 24 '21 at 04:13
  • $h$ is the x-coordinate of the center, $k$ is its y-coordinate, and $r$ is the side length. – Anas Khaled Mar 24 '21 at 04:14
  • Okay thanks, I actually used the midpoint values as ID's by themselves of the square. Really helped a lot! – flutterbug98 Mar 24 '21 at 05:09