$0$ is the correct derivative, which you got in the first calculation. I assume however that you overlooked something in the calculation, as the limit is far from simple.
When evaluating the derivation limit directly, you correctly get that it is the limit of a product of 3 terms:
$$f'(1)=\lim_{x\to 1}(x-1)^{-2/3}(x-2021)^{1/3}|\sin(\pi x)|$$
Now the 'easy' solution to this would be if we could calculate the limit of each term directly, then multiply their results. But it turns out this doesn't work, as one term tends to infinity:
$$\lim_{x\to 1}(x-1)^{-2/3} = \infty,$$
$$\lim_{x\to 1}(x-2021)^{1/3} = \sqrt[3]{-2020},$$
$$\lim_{x\to 1}|\sin(\pi x)| = 0,$$
the last 2 limits calculated simply be realizing that the functions taken to the limit are continuous at the given point. So one limit is $\infty$, one is $0$ and one is a finite, non-zero number. That means the limit of their product could be anything: $0$, some other number, $\infty$ or "diverging" in the strict sense (not tending to a finite number or infinity). We need to evaluate the limit of the product
$$\lim_{x\to 1}(x-1)^{-2/3}|\sin(\pi x)|,$$
and whatever we find as a result (if there is one at all), it will just have to be multplied by $\sqrt[3]{-2020}$ in order to get the derivative.
Now we have
$$(x-1)^{-2/3}|\sin(\pi x)| = \frac{|\sin(\pi x)|}{(x-1)^{2/3}} = \frac{|\sin(\pi x - \pi)|}{(x-1)^{2/3}} = \frac{|\sin(\pi(x - 1))|}{(x-1)^{2/3}} = (x-1)^{1/3}\frac{|\sin(\pi(x - 1))|}{(x-1)} = \pi(x-1)^{1/3}\frac{|\sin(\pi(x - 1))|}{\pi(x-1)}.$$
These are mostly simple equivalent transformations, where the fact that $|\sin(x)|$ has period $\pi$ has ben used for the second equality sign.
Now if you've seen a bit of trigonometric limits, the last term contains a part that is very near to what you may have seen before, if you set $y=\pi(x-1)$
$$\lim_{y\to 0}\frac{\sin(y)}y = 1$$
The only difference is that our term contains an absolute value. But that absolute value doesn't change that
$$\frac{|\sin(\pi(x - 1))|}{\pi(x-1)}$$
is bounded around $x=1$. So we see that
$$\pi(x-1)^{1/3}\frac{|\sin(\pi(x - 1))|}{\pi(x-1)}$$
is the product of 2 factors, the first of which ($\pi(x-1)^{1/3}$) tends to $0$ when $x\to 1$ and the second ($\frac{|\sin(\pi(x - 1))|}{\pi(x-1)}$) stays bounded when $x \to 1$. That means the product of those 2 functions tends to $0$ as well:
$$\lim_{x \to 0}\pi(x-1)^{1/3}\frac{|\sin(\pi(x - 1))|}{\pi(x-1)} = 0.$$
That finally means that
$$f'(1)=\lim_{x\to 1}(x-1)^{-2/3}(x-2021)^{1/3}|\sin(\pi x)| = \lim_{x \to 0}\pi(x-1)^{1/3}\frac{|\sin(\pi(x - 1))|}{\pi(x-1)} \times \lim_{x\to 1}(x-2021)^{1/3} = 0 \times \sqrt[3]{-2020}=0.$$
Now what happened when using the second method to calculate the derivative explicitly?
The function $f$ is given as the product of 2 functions, and it turns out that neither factor is differentiable at $x=1$. You can do the calculations yourself (you did already), but the Wolfram alpha picutures show that the root part has an "infinite" derivative:
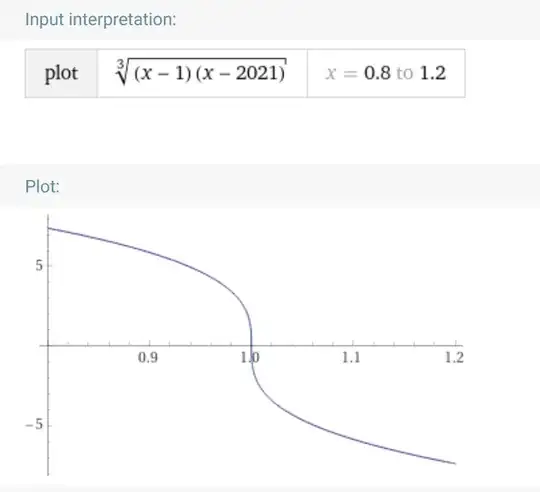
The $\sin$ part OTOH has different left and right derivates (due to the absolute value function "flipping" the sin function at $x=1$):
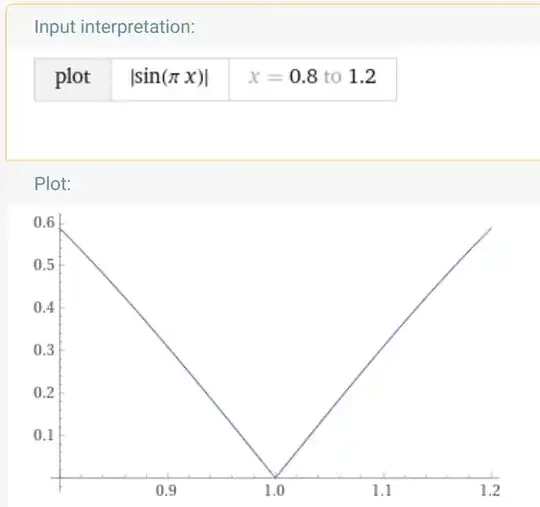
So you simply can't use the product rule for the function at the point $x=1$, because that requires that both functions have a derivative at that point, which isn't true. One would guess that the product of 2 such functions would then also have no derivative for $x=1$, but the above calculation shows that is not true.
Finally, here comes the picture of how the function $f$ looks like around $x=1$:
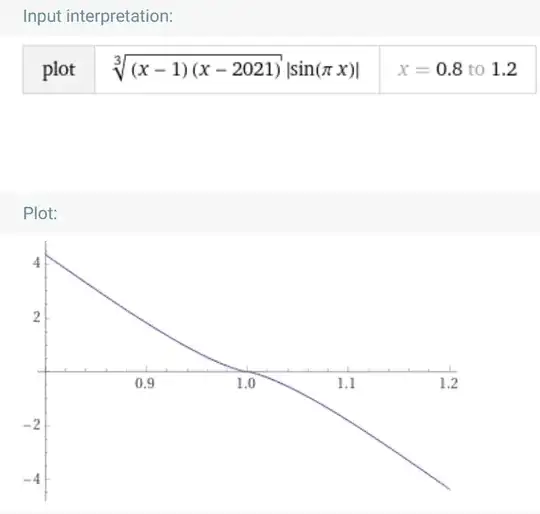
It looks continuous, though one can't really see what the derivative at $x=1$ is, but that cleared up by the above calculation.


