Desmos plot only for integral $x$

Question

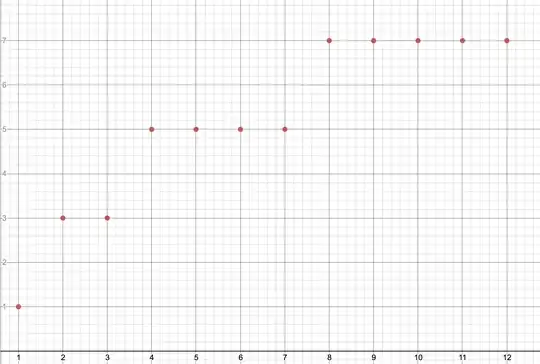
I'm trying to plot $2\operatorname{floor}\left(\log_{2}x\right)+1$ but only if $x$ is a natural number.
Desmos plots correctly
$2\operatorname{floor}\left(\log_{2}x\right)+1$

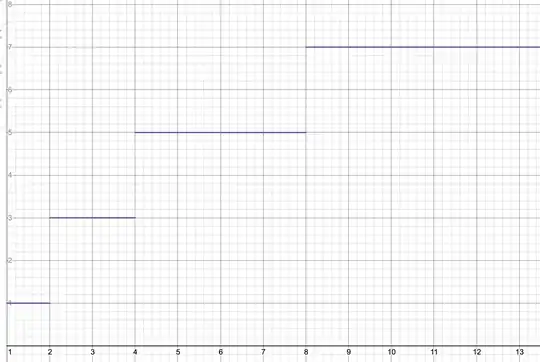
I would like this however:

I achieved this using a list of points $[(1,1),(2,3),(3,3),(4,5)\ldots]$ but I would like to plot up to infinity and I don't think desmos supports list comprehensions like that.

So instead I tried using desmos-style piecewise functions like $y=\left\{\operatorname{mod}\left(x,1\right)=0:2\operatorname{floor}\left(\log_{2}x\right)+1\right\}$ but this has no output at all.

So, how can I create a graphic like the second for all natural $x$? (At least up to $x=2^{2700}$)

@SujitBhattacharyya if you yourself have tried that, you would know that it does not satisfy what OP is looking for. — Andrew Chin, Mar 22 '21 at 07:14

score 4 · Accepted Answer · answered Mar 22 '21 at 07:29

4

This will get you what you want.

The idea is to define a function, then plot points using a list.

In this case, we define a function $$f(x)=2\text{floor}(\log_2x)+1$$ and make the calculator plot points $(a,f(a))$ where $a\in(1,2,3,...)$.

answered Mar 22 '21 at 07:29

Andrew Chin

7,389

How do I use the list of natural numbers for $a$? – minseong Mar 22 '21 at 07:31
Define it explicitly as a list in one of the fields available. – Andrew Chin Mar 22 '21 at 07:32
Absolutely perfect. Thanks for the answer I was also trying to find a solution found one but it was only limited to 100 numbers. Thanks again. – Sujit Bhattacharyya Mar 22 '21 at 07:33
I'd like to go up to at least 2^2700 – minseong Mar 22 '21 at 07:37
upvoted both the ques and ans – Sujit Bhattacharyya Mar 22 '21 at 07:40

Desmos plot only for integral $x$

1 Answers1