Does $\lim_{k \to \infty}[(\sum_{n=1}^{k}\frac{1}{n})-\ln k]$ exists?

Question

Let $k>2$, is a natural number, does $\lim_{k \to \infty}[(\sum_{n=1}^{k}\frac{1}{n})-\ln k]$ exists? If $k \to \infty$, then I think no, because $\ln k$ will go to infinite. And $\sum \frac{1}{n}$ diverge too, and so it's $\infty - \infty$. But someone say the limit exists? and it's positive. How?

Answer 1

Yes. It's called the Euler-Mascheroni constant and it is positive. This is because the harmonic numbers are approximately logarithmic so the difference between them is small.

Answer 2

Note that $$ - \log k = - \log \left( {\frac{2}{1} \cdots \frac{{k - 1}}{{k - 2}}\frac{k}{{k - 1}}} \right) = - \sum\limits_{n = 2}^k {\log \left( {\frac{n}{{n - 1}}} \right)} = \sum\limits_{n = 2}^k {\log \left( {1 - \frac{1}{n}} \right)} . $$ Thus, $$ \sum\limits_{n = 1}^k {\frac{1}{n}} - \log k = 1+\sum\limits_{n = 2}^k {\left( {\frac{1}{n} + \log \left( {1 - \frac{1}{n}} \right)} \right)} . $$ Now if $0<x\leq \frac{1}{2}$, then $$ \left| {x + \log (1 - x)} \right| = \left| { - \int_0^x {\frac{t}{{1 - t}}dt} } \right| \le 2\int_0^x {tdt} = x^2 . $$ Therefore, $$ \left| {\sum\limits_{n = 2}^k {\left( {\frac{1}{n} - \log \left( {1 - \frac{1}{n}} \right)} \right)} } \right| \le \sum\limits_{n = 2}^k {\left| {\frac{1}{n} - \log \left( {1 - \frac{1}{n}} \right)} \right|} \le \sum\limits_{n = 2}^k {\frac{1}{{n^2 }}} < \sum\limits_{n = 2}^\infty {\frac{1}{{n^2 }}} < \infty . $$ Consequently, the sequence $$ 1 + \sum\limits_{n = 2}^k {\left( {\frac{1}{n} - \log \left( {1 - \frac{1}{n}} \right)} \right)} = \sum\limits_{n = 1}^k {\frac{1}{n}} - \log k $$ is convergent.

Answer 3

$$\sum_{n=1}^{k}\frac{1}{n}$$ is the sequence of harmnonic numbers (of order 1).

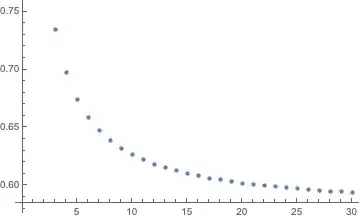
This is a plot of the starting of the minuends/subtrahents under consideration:

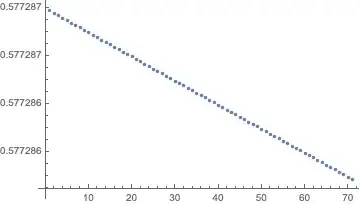
This plot shows the starting of the difference:

This looks by graphical representation pretty convergent.

The limit can be representated as the riemannian sum limit of the difference of two integrals the second one as riemannian sum, the as easy integral: $$\lim_{k\rightarrow\infty}(-ln(k)+\sum_{n=1}^{k}\frac{1}{n})=\int_{1}^{\infty}(\frac{1}{x}-\frac{1}{\lfloor x\rfloor})=\gamma=0.577216$$ $\lfloor x\rfloor$ represents the floor function. This page show a lot more information about the Euler Mascheroniconstant and that this identity stems from L. Euler himself. The proof is rather easy because the integral is over this

A step size below 1 does not change anything. It is a stair function in the denominator. The riemannian sum approximation is exact for stair functions.

Despite the exact representation this is not a formlar for calculating the Euler-Mascheroni-constant depsite up to some decimals. The name of the differnce is convention and the numerical value an reals with only approcimate represenations.

The convergence is really slow but this picture is one the is the really famous signature of the convergence as example between 7030 and 7100 is looks still nice convergent

This is exact to the 5th decimal.

Mind the the first term in the middle of my equation chain does not exist alone. So this is indeed an instruction to calculate the Euler-Mascheroni-constant numerical. The riemannian theory of integrals gave it a new meaning centuries later.

Both term of the difference are each divergent but with a finite value at infinity. That is really strange despite it is clear by the graphics and by the continous decline of the difference and the lower limit given by the x-axis. The sequence of the difference is strictly monotonous decrease and has a lower limit, so is it convergent. Rules valid in general found here, Limit of a sequence.

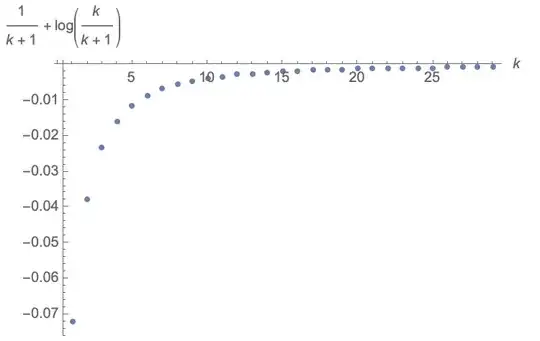
$$\frac{1}{k+1}+ln(k)-ln(k+1)<0 : \forall k>2$$

$$\frac{1}{k+1}>-ln(k)+ln(k+1)=ln(\frac{k+1}{k})=ln({1+\frac{1}{k}) : \forall k>2$$

$ln(x)$ is divergent and there monotonous increasing. Therefore is always $ln(k+1)>ln(k)$ for all integer $k$. $\frac{1}{x}$ in monotonous decrease and converges towards $0$. To add this to $ln(k)$ does not enlarge the value large enought to get bigger than $ln(k+1)$.

This is initially verifiable by

The sequence is elementwise positive. This can be infered by the first plot of my answer and the fact that both a monotonously increasing. All increase are strict. From sentences about steady functions with one know order at point and the knowledge that both are strictly increasing follows the condition if fullfilled.

That is all needed. This can be put into statements with quantors.