Splitting a circle into 3 equal parts using 2 lines

Question

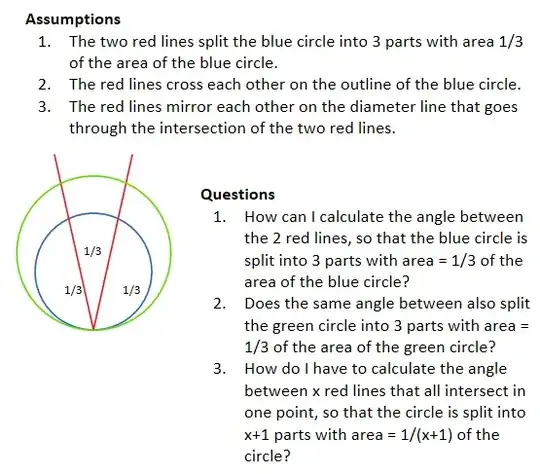
The picture probably explains my question best.
I need to find a way to divide a circle into 3 parts of equal area with only 2 lines that intersect each other on the outline of the circle.
Also I need to check, if whatever diameter is between those lines, also splits circles with a different diameter into equal parts.
And lastly, and probably the most difficult question: How do I have to calculate the angle between x lines that all intersect in one point, so that the circle is split into x+1 parts with area = 1/(x+1) of the circle?
I tried my best, but couldn't even find a single answer or the right strategy to tackle the question...

1

Answer 1

1. To find the angle $x$ between the red lines you need to solve the equation $$\sin(x)+x=\frac\pi3.\tag1$$ This can be done only numerically.

2. Yes it divides also the green circle in three equal parts.

3. Observe the essential difference between the cases with even and odd $n$. Whereas in former case the diameter drawn from the common intersection point is one of the "red" lines, in the latter case it is the bisector of the central angle. Let $x_k$ be the angle of a red line with the diameter. Then the following are the equations to find $x_k$: $$ x_k+\frac12\sin2x_k=\frac\pi{n}k, \quad\text{with}\quad k=-\frac n2+1\dots \frac n2-1.\tag2 $$ Observe that the numbers $k$ are integer for even $n$ and half-integer for odd $n$. For $n=3$ the equation $(2)$ reduces to $(1)$ with $x=2x_\frac12$.

Answer 2

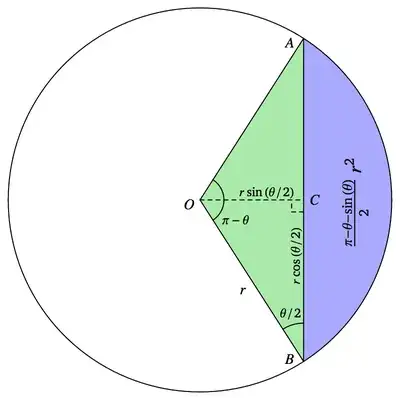
Given the angle $\theta$, split by the diameter containing $B$, consider the following diagram:

$\overline{BO}$ is the line through the center and $\overline{BA}$ is the chord cutting off the lune whose area we wish to compute.

The area of the circular wedge subtended by $\angle BOA$ is $$ \frac{\pi-\theta}2r^2\tag1 $$ The area of $\triangle BOA$ is $$ \frac12\cdot\overbrace{r\sin\left(\frac\theta2\right)}^\text{altitude}\cdot\overbrace{2r\cos\left(\frac\theta2\right)}^\text{base}=\frac{\sin(\theta)}2r^2\tag2 $$ Therefore, the area of the lune is $(1)$ minus $(2)$: $$ \frac{\pi-\theta-\sin(\theta)}2r^2\tag3 $$ To get the area divided into thirds, we want $$ \frac{\pi-\theta-\sin(\theta)}2r^2=\frac\pi3r^2\tag4 $$ which means we want to solve $$ \theta+\sin(\theta)=\frac\pi3\tag5 $$ whose solution can be achieved numerically (e.g. use $M=\frac\pi3$ and $\varepsilon=-1$ in this answer) $$ \theta=0.5362669789888906\tag6 $$ Giving us

---

Numerical Details

The iteration from this answer, applied to $\theta+\sin(\theta)=\frac\pi3$, is $$ \theta_{n+1}=\frac{\pi/3-\sin(\theta_n)+\theta_n\cos(\theta_n)}{1+\cos(\theta_n)}\tag7 $$ Here is the result of this iteration starting at $0$; $$ \begin{array}{l|l} n&\theta_n\\\hline 0&0\\ 1&0.5\color{#AAA}{23598775598298873077107230547}\\ 2&0.5362\color{#AAA}{45321326153808318904236597}\\ 3&0.5362669789\color{#AAA}{24456230942633093381}\\ 4&0.53626697898889055276\color{#AAA}{1878717471}\\ 5&0.53626697898889055276244906787\\ 6&0.53626697898889055276244906787 \end{array} $$

Answer 3

Connect the ends of the chord (red line) with the center. You get isosceles triangle. Let $x$ be the angle opposite to the base (i.e. chord) in that triangle. You want: $$\frac{r^2x}{2}-\frac{r^2 \sin x}{2}=\frac{r^2\pi}{3}$$ or $$x-\sin x=\frac{2\pi}{3}$$ I do not think it can be solved analytically but it can be solved numerically with the answer $x \approx 2.60533$ radian. The same logic can be applied to more than 3 pieces. The angle you are looking for is $\pi-x$

Answer 4

Too long for comments

If you want to solve $$\theta+\sin(\theta)=\frac\pi3$$ what you can do is to expand the lhs as a Taylor series and use series reversion. Using ths simple $$y=\theta+\sin(\theta)=2 \theta -\frac{\theta ^3}{6}+\frac{\theta ^5}{120}-\frac{\theta^7}{5040}+O\left(\theta ^9\right)$$ this would give $$\theta=\frac{y}{2}+\frac{y^3}{96}+\frac{y^5}{1920}+\frac{43 y^7}{1290240}+O\left(y^9\right)$$ Making $y=\frac \pi 3$ and computing $$\theta=0.53626300$$

You could also use the $1,400$ years old approximation $$\sin(\theta) \simeq \frac{16 (\pi -\theta)\theta}{5 \pi ^2-4 (\pi -\theta) \theta}\qquad (0\leq \theta\leq\pi)$$ and solve the cubic $$-\frac{5 \pi ^3}{3}+\pi\left(16 +\frac{19 \pi }{3}\right) \theta-16\left(1+\frac{\pi }{3}\right) \theta^2+4 \theta^3=0$$ which shows only one real root (not very nice formal expression) which is $0.53631167$.

Since, by inspection, you know that the solution is close to $\frac \pi 6$, you could perform one single iteration of Newton-like method and have explicit approximations which will be better and better increasing the order $n$ of the method. For example, Newton method would give $$\theta_{(2)}=\frac \pi 6+\frac{1}{3} \left(2-\sqrt{3}\right) (\pi -3)$$ Halley method would give $$\theta_{(3)}=\frac \pi 6+\frac{2 \left(2+\sqrt{3}\right) (\pi -3)}{45+24 \sqrt{3}-\pi }$$ As a function of $n$, the results would be $$\left( \begin{array}{ccc} n & \text{estimate} & \text{method} \\ 2 & 0.536245321326154 & \text{Newton} \\ 3 & 0.536266784935255 & \text{Halley} \\ 4 & 0.536266978676557 & \text{Householder} \\ 5 & 0.536266978987702 & \text{no name} \\ 6 & 0.536266978988890 & \text{no name} \\ 7 & 0.536266978988891 & \text{no name} \end{array} \right)$$