Mathematica can calculate $e^{-\sqrt{s}}/s^{3/2}$, and the result is $$-1 + \frac{2\sqrt{t} e^{-\frac{1}{4t}}}{\sqrt{\pi}} + \mbox{Erf}\left[\frac{1}{2\sqrt{t}}\right]$$.
However, when I used the residue theorem to calculate it, the integral along the small circle around zero is divergent, $\frac{1}{2\pi i} \int \frac{e^{-\sqrt{s}}}{s^{3/2}} e^{st} ds,\ s=\epsilon e^{i\theta},\ \theta \in(\pi,-\pi) $.
Would you like to help me with this problem? Thanks in advance.
To find the inverse LT, we may use the definition, which requires integration in the complex plane:
$$f(t) = \frac1{i 2 \pi} \int_{c-i \infty}^{c+i \infty} ds \, s^{-3/2} e^{-\sqrt{s}} e^{s t} $$
where $C$ is the following contour:
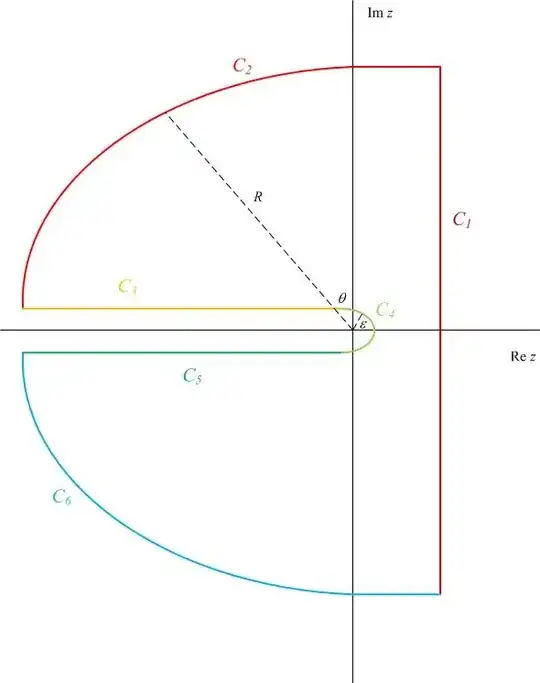
(NB I have used this contour for years and lots of people have relied on it in turn. But please keep in mind that this contour is really an approximation, one that works but is a simplification of the actual contour.)
We will define $\text{Arg}{z} \in (-\pi,\pi]$, so the branch is the negative real axis. There are $6$ pieces to this contour, $C_k$, $k \in \{1,2,3,4,5,6\}$, as follows.
$C_1$ is the contour along the line $z \in [c-i R,c+i R]$ for some large value of $R$.
$C_2$ is the contour along a circular arc of radius $R$ from the top of $C_1$ to just above the negative real axis.
$C_3$ is the contour along a line just above the negative real axis between $[-R, -\epsilon]$ for some small $\epsilon$.
$C_4$ is the contour along a circular arc of radius $\epsilon$ about the origin.
$C_5$ is the contour along a line just below the negative real axis between $[-\epsilon,-R]$.
$C_6$ is the contour along the circular arc of radius $R$ from just below the negative real axis to the bottom of $C_1$.
We will show that the integral along $C_2$,$C_4$, and $C_6$ vanish in the limits of $R \rightarrow \infty$ and $\epsilon \rightarrow 0$.
On $C_2$, the real part of the argument of the exponential is $R t \cos{\theta} + \sqrt{R} \cos{(\theta/2)}$, where $\theta \in [\pi/2,\pi)$. Clearly, $\cos{\theta} < 0$, so that the integrand exponentially decays as $R \rightarrow \infty$ and therefore the integral vanishes along $C_2$ as:
$$R \int_{\pi/2}^{\pi} d\theta R^{-3/2} e^{R t \cos{\theta}+\sqrt{R} \cos{(\theta/2)}} \le R^{-1/2} \int_0^{\pi/2} d\theta \, e^{-R t \sin{\theta}+\sqrt{R} \sin{\left (\frac{\pi}{4}-\frac{\theta}{2} \right )}} \le \frac{\pi e^{-\sqrt{R}/2}}{2 R^{1/2}(t R - \sqrt{R}/2)} $$
(NB it is assumed in that computation that $R \gt \frac1{4 t^2}$.)
On $C_6$, we have the same thing, but now $\theta \in (-\pi,-\pi/2]$. This means that, due to the evenness of cosine, the integrand exponentially decays again as $R \rightarrow \infty$ and therefore the integral also vanishes along $C_6$.
On $C_4$, The integral behaves as
$$i \epsilon \int_{\pi}^{-\pi} d\phi \, e^{i \phi} \epsilon^{-3/2} e^{-i 3 \phi/2} e^{-\epsilon^{1/2} e^{i \phi/2}}e^{\epsilon e^{i \phi} t} = -i 4 \epsilon^{-1/2} + i 2 \pi + O \left ( \epsilon^{1/2} \right )$$
While this is singular as $\epsilon \to 0$, this divergence will cancel as follows. On $C_3$, we have $z=e^{i \pi} x$ and the integral there is
$$e^{i \pi} \int_R^{\epsilon} dx \, x^{-3/2} e^{-i 3 \pi/2} e^{-i \sqrt{x}} e^{-x t} $$
On $C_5$, we have $z=e^{-i \pi} x$ and the integral there is
$$e^{-i \pi} \int_R^{\epsilon} dx \, x^{-3/2} e^{i 3 \pi/2} e^{i \sqrt{x}} e^{-x t} $$
Combining the two integrals, we get, integrating by parts and as $R \to \infty$,
$$\begin{align}i 2 \int_{\epsilon}^{\infty} dx \, x^{-3/2} \, \cos{\sqrt{x}} \, e^{-x t} &= i 4 \epsilon^{-1/2} \cos{\sqrt{\epsilon}} \, e^{-\epsilon t} - i 4 \int_{\epsilon}^{\infty} dx \, x^{-1/2} \left (\frac{\sin{\sqrt{x}}}{2 \sqrt{x}} + t \cos{\sqrt{x}} \right ) e^{-x t} \end{align}$$
As stated, the divergences cancel and the contour integral is equal to, as $\epsilon \to 0$:
$$\int_{c-i \infty}^{c+i \infty} ds \, s^{-3/2} e^{s t} - i 4 \int_{\epsilon}^{\infty} dx \, x^{-1/2} \left (\frac{\sin{\sqrt{x}}}{2 \sqrt{x}} + t \cos{\sqrt{x}} \right ) e^{-x t} + i 2 \pi$$
Note that the 2nd integral indeed converges. By Cauchy's theorem, the contour integral is zero. Thus, the ILT is
$$\frac1{i 2 \pi} \int_{c-i \infty}^{c+i \infty} ds \, s^{-3/2} e^{s t} = -1 + \frac{2}{\pi} \int_{0}^{\infty} dx \, x^{-1/2} \left (\frac{\sin{\sqrt{x}}}{2 \sqrt{x}} + t \cos{\sqrt{x}} \right ) e^{-x t}$$
The integral on the right is not too bad to evaluate; NB it is easy to show using Parseval's Theorem that
$$\frac{2}{\pi} \int_{0}^{\infty} dx \, x^{-1/2} \frac{\sin{\sqrt{x}}}{2 \sqrt{x}} e^{-x t} = 2 \operatorname{erf}{\left ( \frac1{2 \sqrt{t}} \right )} $$
$$\frac{2}{\pi} \int_{0}^{\infty} dx \, x^{-1/2} t \cos{\sqrt{x}} e^{-x t} = 2 \sqrt{\frac{t}{\pi}} e^{-\frac1{4 t}} $$
Finally, we have the ILT in closed form:
$$\frac1{i 2 \pi} \int_{c-i \infty}^{c+i \infty} ds \, s^{-3/2} e^{-\sqrt{s}} e^{s t} = \frac{2}{\sqrt{\pi}} t^{1/2} e^{-\frac1{4 t}} - \operatorname{erfc}{\left ( \frac1{2 \sqrt{t}} \right )} $$
