What is the function for the probability distrabution of rolling multiple (3+) dice. The function is a bell curve but I can't find the actual function for the situation. Example, what is the function for rolling 50 6 sided dice?
EDIT: A six sided die returns an integer value from 1 to 6 inclusive. I am trying to find a function to add multiple dice together.
In this answer, there is a section titled "Summing Dice". It describes how convolution of the discrete function that is $1$ for each integer from $1$ through $6$, and $0$ otherwise, yields the distribution for the sum of $n$ six-sided dice.
Rolling $50$ six-sided dice will yield an approximately Normal Distribution whose mean is $\mu=50\times\frac72$ and whose variance is $50\times\frac{35}{12}$; thus, a standard deviation of $\sigma=\sqrt{50\times\frac{35}{12}}$.
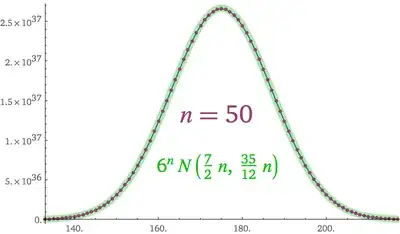
Mean and Variance of a Single Die
The mean of a single die whose faces vary from $1$ to $n$ is $\frac{n+1}{2}$. For $n=6$, this gives $\frac72$.
The variance of a single die whose faces vary from $1$ to $n$ is "the mean of the squares minus the square of the mean." The sum of the squares from $1$ to $n$ is $\frac{2n^3+3n^2+n}{6}$, so the mean is $\frac{2n^2+3n+1}{6}$. Subtracting $\frac{n^2+2n+1}{4}$ yields $\frac{n^2-1}{12}$. For $n=6$, this gives $\frac{35}{12}$.
