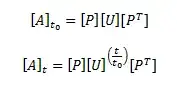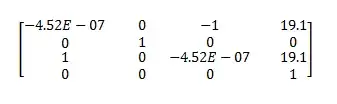0

I am making a 3D graphics processor using VB.Net.

I want to do an airplane game.

I want the plane(s) movements to be scalable by time, so that the appearance is the same regardless of how fast the game-loop is running. And so the amount of matrix & trig operations needed per frame is minimized.

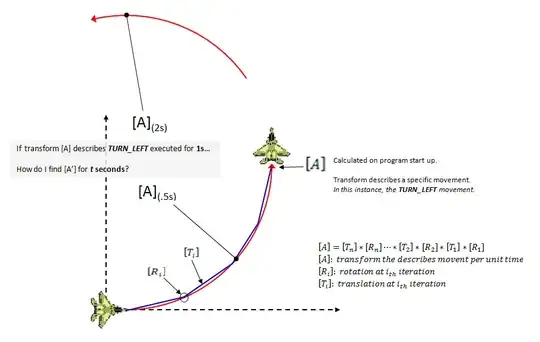
Below is a 2D example of what I am trying to achieve.

enter image description here

I'm trying to do eigen-decomposition so a can scale transform A by time:

enter image description here

  • I figure out a complex movement (like turning left) using many small iteration steps at the start of the program.
  • Solving for the largest eigen-vector & its value using the power iteration
  • Other stuff to find the other eigen-vector(s) & values (still haven't nailed that down yet)
  • Now, with this transform-decomposition for the turn-left operation for T seconds of game time, I can compute turn-left transforms for any time duration quickly and easily.

Ran into problems fast with a simple translation matrix that does not decompose. Then I saw this: Decomposing an Affine transformation This guy apparently did it but did not show how. I know its going to involve complex eigenvalues (if you got things rotating). Im not sure how to handle those. And it is going to involve seperating the translation part, which I also don't know how to do.

Here is 2 examples that I would like to see how to solve:

Simple X translation

Rotating and translating

The whole point is to avoid doing hundreds of movement iterations at every game frame. The example shown has an easy solution for scaling by time, rotating around the arc center by x*dt. But, when I start doing combinations of 3D rotations like TURNING-UP while also TURNING-RIGHT while also ROLLING (cork-screwing in circle) it is going to be extremely time consuming figuring how to scale these movements by time.

I want the computer to do all the math.

Tony
  • 111

1 Answers1

1

Combining my answer on interpolation with another answer on matrix logarithm / exponential:

import numpy as np
from scipy.linalg import logm, expm

A = np.array([[1, 0, 0, 30],
              [0, 1, 0,  0],
              [0, 0, 1,  0],
              [0, 0, 0,  1]])
logA = logm(A)
print(logA)
for t in range(0, 11):
  print(expm(t * 0.1 * logA))


B = np.array([[-4.52e-7, 0, -1      , 19.1],
              [ 0      , 1,  0      ,  0  ],
              [ 1      , 0, -4.52e-7, 19.1],
              [ 0      , 0,  0      ,  1  ]])
logB = logm(B)
print(logB)
for t in range(0, 11):
  print(expm(t * 0.1 * logB))

https://ideone.com/bnNBqb has the numbers if you want them.

If you want to avoid the matrix logarithm, then you suffer from the problem that the first of the two matrices you gave is not diagonalizable.

Whether computing these matrix exponentials is indeed faster than the transformation you want to avoid is a question you need to answer for your application.

MvG
  • 42,596