0

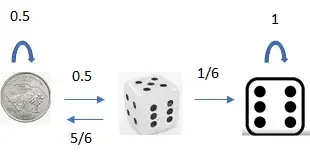
Assume a coin and a six-sided die. At the first move, you flip a coin. If you get a heads, you get to roll the die. If you get a tails, you have to flip the coin again. When you roll the die, if you get a $6$, the game is over. If you don't get a $6$, you have to flip the coin again. What is the probability of getting a $6$ on the die within $6$ moves? Each coin flip or die roll is a move.

I tried it with $4$ moves using brute force method with a tree diagram, and found an answer of $4$ in $60$, or $1$ in $15$. What I want to know is the general solution of this game within $n$ moves.

Jessie
  • 1,463
Franklin Xander
  • 1

2 Answers2

1

We are going to compute the complimentary probability $p_n$ that there are no $6$ in $n$ moves. Note that there is a special case when we throw a head in the last move. If the move was not the last we were ought to throw a die but in this "defect" case it is not allowed.

Let us assume that $k$ heads was thrown in $n$ moves. In the normal case this means that there were $n-2k$ tails which amounts together to $n-k$ coins, which we can permute in $\binom{n-k}k$ ways. In the defect case we will similarly obtain $n-2(k-1)-1=n-2k+1$ tails and $(n-2k+1)+(k-1)=n-k$ coins which we can arbitrarily permute (plus one additional coin which position is fixed). Plugging everything together we will obtain the probability: $$ \binom{n-k}k \left(\frac56\right)^k\left(\frac12\right)^{n-k}+\binom{n-k}{k-1} \left(\frac56\right)^{k-1}\left(\frac12\right)^{n-k+1}. $$

The total possibility can be computed by summing over all possible values of $k$: $$ p_n=\frac1{2^n}\sum_{k=0}^{\left\lceil\frac n2\right\rceil} \binom{n-k}k\left(\frac53\right)^k+\binom{n-k}{k-1}\left(\frac53\right)^{k-1},\tag1 $$ and $1-p_n$ will then give the probability to finish the game in $n$ moves.

Applying the formula $(1)$ to the case $n=4$ one obtains the value $$ 1-p_n=\frac{13}{72} $$ which differs from your calculation but agrees with my check: $$ \begin{array}{l|l} XXXX& p\times\frac16\\ \hline H6& \frac12\\ H\bar6H6&\frac12\frac56\frac12\\ TH6&\frac12\frac12\\ TTH6&\frac12\frac12\frac12\\ \hline &\frac{13}{12} \end{array}$$

user
  • 26,272
0

We can use Markov transition matrix to solve this problem in general. Repeating the following procedure n times to get the probability to roll 6 to exit (for example, when n = 4, the probability is shown in the last row in $S_4$ below to be $\frac{13}{72}$). $\to$

Set up the transition matrix T and initial state $S_0$, then calculate the next state with thie formula

$S_{i+1}$=T.$S_i$ (where i =0,1,2,3...).

enter image description here

$T= \begin{bmatrix} 0.5&\frac{5}{6}& 0 \\ 0.5&0 & 0\\0&\frac{5}{6}&1 \end{bmatrix}$ $S_0= \begin{bmatrix} 1 \\0\\0 \end{bmatrix}$

$S_1=T.S_0 = \begin{bmatrix} 0.5\\0.5\\0 \end{bmatrix}$

$S_2=T.S_1 = \begin{bmatrix} \frac{2}{3}\\\frac{1}{4}\\\frac{1}{12} \end{bmatrix}$

. $S_3=T.S_2 = \begin{bmatrix} \frac{13}{24}\\\frac{1}{3}\\\frac{1}{8} \end{bmatrix}$

$S_4=T.S_3 = \begin{bmatrix} \frac{79}{144}\\\frac{13}{48}\\\frac{13}{72} \end{bmatrix}$

Star Bright
  • 2,338