$X\vee Y\cong (X\times\{y_0\})\cup (\{x_0\}\times Y)$

Question

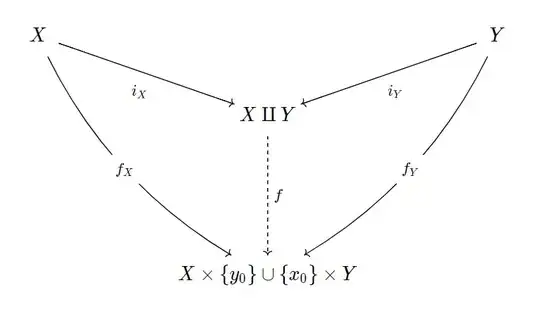
Let $(X,x_0),(Y,y_0)$ be two pointed topological spaces. Then $X\vee Y$ obtained by $X\amalg Y/x_0\sim y_0$ where $X\amalg Y$ denote the disjoint union of topological spaces and $X\times\{y_0\}\cup \{x_0\}\times Y\subset X\times Y$: subspace are homeomorphic.

My plan to prove this is first by using the universal property of $X\amalg Y$ to get a continuous map $f:X\amalg Y\to X\times\{y_0\}\cup \{x_0\}\times Y$ which is also quotient map so that the induced map from $X\vee Y\to X\times\{y_0\}\cup \{x_0\}\times Y$ is a homeomorphism.

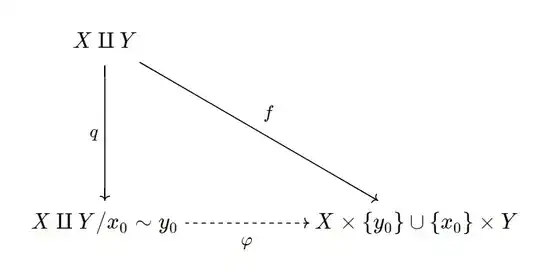I first defined $f_X(x) = (x,y_0)$ and $f_Y(y) = (x_0,y)$ and before checking this map is continuous, I tried to prove this map is open (which is slightly stronger than what we desired). If we take an open set $U\amalg V$ where $U\subset X$ and $V\subset Y$ are open sets, then $f(U\amalg V) = U\times\{y_0\}\cup \{x_0\}\times Y$. Since for $A\subset X,B\subset Y$, $(A\times B)\cap (X\times\{y_0\}\cup\{x_0\}\times Y) = (U\times (V\cap\{y_0\}))\cup((U\cap\{x_0\})\times V)$, to show the map $f$ is open, we need to show $U\times\{y_0\}$ is open in $X\times\{y_0\}\cup \{x_0\}\times Y$ which is not true in general. I hope this is a quotient map then but I can't see. Could you help? or any other idea?

Answer 1

Your map $f$ defined via $f_X$ and $f_Y$ is clearly continuous and induces a continuous bijection $\varphi : X \vee Y \to X\times\{y_0\}\cup \{x_0\}\times Y$.

Now let $U \subset X \vee Y$ be open. Then $q^{-1}(U)$ is open in $X \sqcup Y$ and can be written as $V_X \sqcup V_Y$ with open $V_X \subset X$ and open $V_Y \subset Y$. We have $$\varphi(U) = \phi(q(q^{-1}(U))) = f(q^{-1}(U)) = f(V_X \sqcup V_Y) = f_X(V_X) \cup f_Y(V_Y) \\= V_X\times\{y_0\}\cup \{x_0\}\times V_Y .$$ We shall show that this set is open in $ X\times\{y_0\}\cup \{x_0\}\times Y$. Let $* \in X \vee Y$ denote the common equivalence class of $x_0, y_0$.

Case 1 : $* \in U$. Then $x_0 \in V_X, y_0 \in V_Y$. The set $D = (V_X \times V_Y) \cap (X\times\{y_0\}\cup \{x_0\}\times Y)$ is open in $X\times\{y_0\}\cup \{x_0\}\times Y$. We have $$D = (V_X \times V_Y) \cap (X\times\{y_0\}) \cup (V_X \times V_Y) \cap (\{x_0\}\times Y) = V_X \times \{y_0\} \cup \{x_0\} \times V_Y .$$

Case 2: $* \notin U$. Then $x_0 \notin V_X, y_0 \notin V_Y$. The set $E = (V_X \times Y \cup X \times V_Y) \cap (X\times\{y_0\}\cup \{x_0\}\times Y)$ is open in $X\times\{y_0\}\cup \{x_0\}\times Y$. We have $$E = (V_X \times Y) \cap (X\times\{y_0\}) \cup (V_X \times Y) \cap (\{x_0\}\times Y) \\ \cup (X \times V_Y) \cap (X\times\{y_0\}) \cup (X \times V_Y) \cap ( \{x_0\}\times Y) \\= V_X \times \{y_0\} \cup \emptyset \cup \emptyset \cup \{x_0\} \times V_Y .$$

Remark:

The induced $\varphi$ is a bjection for any topology on $X \vee Y$. If $X \vee Y$ has the quotient topology with respect to $q$, then $\varphi$ is continuous. If we look closer to this part, we see that the proof does not require the continuity of $q$, but only the implication $q^{-1}(U)$ open $\Rightarrow U$ open.

Note that our above proof that $\varphi$ is an open map did not use that $X \vee Y$ has the quotient topology with respect to $q$, it works for any topology making $q$ continuous. But in fact the quotient topology is just the finest topology making $q$ continuous.