1

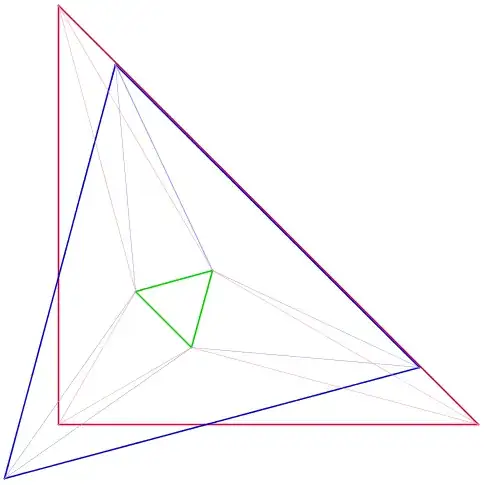
Definition 1. If T is a triangle, let E(T) be the triangle formed by the intersections of the adjacent trisectors of the (interior) angles of T. Synonymously, E(T) will be called the Morley triangle for T.

Remark. By the theorem known as “Morley’s Miracle”, E(T) is always equilateral.

Motivation: I think it is a fairly natural and appropriate question to ask in its own right, but in fact for me it is a stepping stone (provided that the answer is in the affirmative) of another question that is the one that I REALLY want to ask. I don’t know whether it is appropriate for a user to “cascade” questions in a single post, but I’ll go ahead and do so. If it is not appropriate, please let me know. In that case the question that follows can be ignored as an official question for now, and regarded as simply part of the background/motivation for the present question.

While adding entries to the “what surprised you” community wiki, I noticed that one of the entries was on covering an equilateral triangle with squares. Here is the link:

Which one result in mathematics has surprised you the most?

The heads-up on this fascinating result (“One surprise for me – What is the optimal way to cover an equilateral triangle with two squares? It wasn’t solved correctly until 2009. https://erich-friedman.github.io/packing/squcotri/ ”) is due to Silas Pike.

I immediately wondered whether there was a way to relate this to Morley’s Miracle. So, here is what I came up with:

Definition 2. For each positive integer n, let f(n) be the maximal positive number s such that an equilateral triangle of side of length s can be covered by n unit squares.

Definition 3. For each positive integer n, let g(n) be the area of any triangle T such that E(T) has side of length f(n). (Notice that for g to be well-defined requires an affirmative answer to the official question of this post.)

Question: What is the behavior of g? (i.e., “What does its graph look like?”) Is it logarithmic, or exponential, or what? THAT’S what I really wanted to ask.

Regards,

Mike Jones

22.May.2011 (Beijing time)

hardmath
  • 37,015
Mike Jones
  • 4,460

1 Answers1

8

I will take the question in the title:

Can you go backwards from a Morley triangle?

The simple answer is no. Start with any asymmetric triangle, and find its Morley triangle. There is an equilateral triangle which also gives the same Morley triangle (just put a triangle with angles $4\pi/9$, $4\pi/9$, and $\pi/9$ on each edge of the Morley triangle to find its vertices), so the Morley triangle does not define the shape of the original triangle.

An example of an equilateral triangle and a half-square with the same Morley triangle: Morley triangle

Henry
  • 157,058