Examining recurrence relation for its limit and

Question

I have got the following problem:

Examine why the following sequence is well-defined, determine whether it is a monotonous sequence and calculate its limit:

$$a_0 = 3, a_{n+1} = \sqrt{2a_n - 1}$$

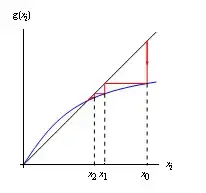
Now just by looking at this sequence and checking its first few entries it seems obvious that it is strictly decreasing. I then proved this with induction. Now I'm trying to find the limit, it seems obvious that its $1$, but I have been struggling to prove this. Since I know the sequence is strictly decreasing I looked at the following:

$$a_n > a_{n+1}$$ $$a_n > \sqrt{2a_n - 1}$$ $$a_n^2 > 2a_n - 1$$ $$a_n^2 - 2a_n + 1 > 0$$ $$(a_n - 1)^2 > 0$$

From this we get that $a_n > 1$ for all n. Would this be a correct proof that the limit of the sequence is 1? And as for whether the sequence is well-defined, since all entries are bigger that $1$ the square root will never have negative input, so it would be well-defined. Would this also be correct?

Answer 1

First you should prove that the sequence is bounded, and thus converge (decreasing + bounded).
Then to find the limit you can set $lim_{n\to\infty} \space a_n = L$ and since $lim_{n\to\infty} \space a_n=lim_{n\to\infty} \space a_{n+1}$

$$ a_{n+1} = \sqrt{2a_n-1} \Longrightarrow lim_{n\to\infty} \space a_{n+1} = \sqrt{2(lim_{n\to\infty} \space a_n)-1}$$ $$\Longrightarrow L=\sqrt{2L-1} \Longrightarrow L^2-2L+1=0 \Longrightarrow L=1$$

Answer 2

The other answer explain you the computation of the limit, but let me add little bit intuition to it. There are plenty of similar problems you can find here with different recurrence relations and almost all of them are actually examples of fixed-point iterations. This is a very useful computational/approximation tool in numerical analysis. In particular, in you problem, we have $x_{n+1}=g(x_n),\quad x_0=3$ with $g(x)=\sqrt{2x-1}.$

So, you start with (given) $x_0,$ feed it in to $g$ and compute $x_1.$ Then feed it again to $g$ and compute $x_2,$ and continue this process forever. For a "nice enough" function $g$ the sequence $x_0, x_1, x_2, \cdots$ converge a limit $L.$ The picture looks roughly like this:

Though $y=x$ is actually the tangent to $y=g(x)$ at $x=1,$ this attracting behavior still holds.

Since the sequence is decreasing and seems converges to $1,$ we can focus on the restricted function $g : [1, 3]\to [1,\sqrt{5}].$ Clearly $g$ is increasing and $g'(x)<1$ for all $x>1,$ which is "nice enough" for the existence of a fixed point.