How do I generalize the connected sets in $\mathbb{R}^2$ if there is a way. I know how connected sets in $\mathbb{R}$ look like, so is there a way to say something about the connected sets in $\mathbb{R}^2$?
-
I don't quite understand what you're asking. Are you asking for a way of defining connected sets in $\mathbb{R}^2$? Or are you asking for something like a classification? The latter would be rather hopeless. – Thorgott Mar 09 '21 at 01:40
-
We can classify the connected subsets of $\mathbb{R}$ as intervals and points. Sadly, there is no generalization to higher dimensions. – JLinsta Mar 09 '21 at 01:42
-
Many times, my intuition for "connected" in $\mathbb{R}$ more closely aligns with "convex" in $\mathbb{R}^n$. – nullUser Mar 09 '21 at 01:45
-
1@AdamRubinson There are connected subsets of $\mathbb{R}^2$ that are not path-connected, i.e. the graph of the topologist's sine curve. – JLinsta Mar 09 '21 at 01:49
1 Answers
There is no good way to classify the connected sets in $\mathbb{R}^2$. Even the planar continua - that is, connected subsets of $\mathbb{R}^2$ which are closed and bounded - are extremely varied (and have a very interesting theory!), see e.g. here.
Now granted, since there isn't a good rigorous notion of "classification" it's hard to turn this into a precise theorem. However, I think the following pretty is pretty definitive:
$(*)\quad$ There are $2^{2^{\aleph_0}}$-many homeomorphism types of connected subsets of the plane. In fact, this is true even for simply connected and path connected subsets!
That is, there are as many distinct "topological types" of connected sets in the plane as there are sets in the plane in the first place! Contrast this with the situation for $\mathbb{R}$, where there are only four.
The proof of $(*)$ is a bit lengthy, but ultimately elementary. Here's one way to do this:
Basically, we want to associate to each set $A$ of paths through the infinite binary tree (there are $2^{2^{\aleph_0}}$-many sets of such paths) an $X_A\subseteq\mathbb{R}^2$ which is connected and such that $A\not=B$ implies $X_A\not\cong X_B$. The first step to doing this is to build a copy of the complete binary tree inside $\mathbb{R}^2$, in a "topologically-decodable" way. For example: 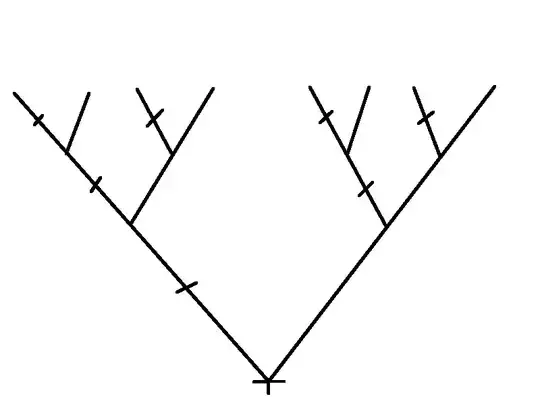
Here the root of the tree is recognizable as the only degree-five point, and we can distinguish left and right via the degree-four points (the little hash marks in the middle of the left-pointing edges). Of course I've only drawn the first few branchings of the tree.
Now we attach, to the "end" of each path through this infinite tree, a copy of $[0,1]$ or $[0,1)$ depending on whether the infinite binary sequence representing that path is in $A$
This is all a little vague; it's a good exercise to fill in the details. Note that the sets so constructed are topologically quite nice in may ways (e.g. contractible, and locally homeomorphic to $\mathbb{R}$ except on a nowhere-dense set).
- 245,398
-
So there are 5 homeomorphisms on $\mathbb{R}$?How did you get this result? – Guria Sona Mar 09 '21 at 01:57
-
@GuriaSona I don't know what that means. There are five connected subsets of $\mathbb{R}$ up to homeomorphism - specifically, if $X$ is a connected subset of $\mathbb{R}$ then $X$ is homeomorphic (as a subspace of $\mathbb{R}$) to one of $\emptyset$ (although there's debate on this point - different reasonable definitions of connectedness disagree about whether the empty space is connected), ${0}$, $[0,1]$, $(0,1)$, and $[0,1)$. – Noah Schweber Mar 09 '21 at 02:00
-
-
1I forgot to mention that there are $c$ many open subsets of ${\mathbb R}^2,$ and so the result in what I cited shows there are as many non-homeomorphic connected open subsets of ${\mathbb R}^2$ as there are open subsets of ${\mathbb R}^2.$ – Dave L. Renfro Mar 09 '21 at 08:31