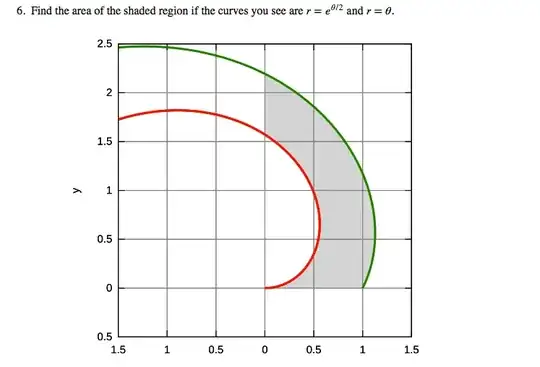
We have to find the area of the region $R$ between $r=\theta $ and $r=e^{\theta/2}$, and between $\theta =0$ and $\theta =\pi /2$. Since the Jacobian of the transformation from Cartesian to polar coordinates is $r$, the area $A$ is given by the double integral (see Explain $\iint \mathrm dx\,\mathrm dy = \iint r \,\mathrm \,d\alpha\,\mathrm dr$):
$$
\begin{eqnarray*}
A &=&\iint_{R}dA=\int_{0}^{\pi /2}\left( \int_{\theta }^{e^{\theta
/2}}r\;dr\right)\ d\theta \\
&=&\int_{0}^{\pi /2}\big( \frac{e^{\theta }}{2}-\frac{\theta ^{2}}{2}
\big)\ d\theta \\
&=&\frac{1}{2}\int_{0}^{\pi /2}e^{\theta }d\theta -\frac{1}{2}\int_{0}^{\pi
/2}\theta ^{2}\ d\theta \\
&=&\big( \frac{e^{\pi /2}}{2}-\frac{1}{2}\big) -\frac{\pi ^{3}}{48}.
\end{eqnarray*}
$$