Product of Consecutive integers problem

Asked Mar 04 '21 at 08:40

Active Mar 04 '21 at 08:50

Viewed 41 times

Product of Consecutive integers problem

I've begun pondering the following problem, and have found myself unable to advance on it; it goes like this:

Prove that the product of three consecutive integers is never the product of two consecutive integers (with a finite number of exceptions).

Now, I basically have very little idea of what to work with. Obviously, I have two exceptions: {1, 2, 3} ($1 \times 2 \times 3 = 2 \times 3$) and {5, 6, 7} ($5 \times 6 \times 7 = 14 \times 15$).

I formed the following equations:

$x(x-1)(x+1) = y(y+1)$

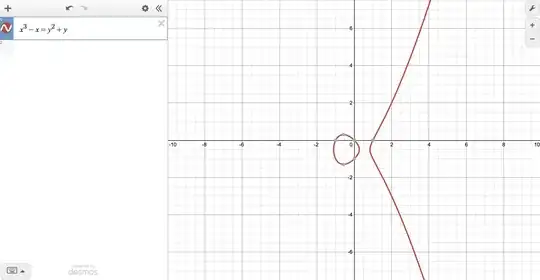
==> $x^3 - x = y^2 + y$

But I have no idea where to go from here. Graphing this on desmos yields the following elliptical curve, which I don't think helps me:

How do I prove/ this conjecture?

edited Mar 04 '21 at 08:50

asked Mar 04 '21 at 08:40

1

What has this to do with [tag:algebraic-geometry]? – José Carlos Santos Mar 04 '21 at 08:45
Apologies, I clicked the wrong one by the looks of it! My bad, will update. – Mar 04 '21 at 08:50
@JoséCarlosSantos does algebra-precalculus work better? I'm not actually sure what facet to put this in. – Mar 04 '21 at 08:51
Fair @TheSimpliFire. – Mar 04 '21 at 08:55
Last time I've looked, elliptic curves were pretty much related to algebraic geometry, so you've done nothing wrong. Some of the old guys here can't suppress their urge to "teach" even when they don't have a clue. – qfwfq Mar 04 '21 at 13:31
Thank you @qfwfq. Good to know. – Mar 04 '21 at 20:42

Product of Consecutive integers problem

Product of Consecutive integers problem

0 Answers0