10

In this wonderful question we learned that a square can be divided into forty six $45^\circ-60^\circ-75^\circ$ triangles.

Now I am wondering what is the smallest number of $45^\circ-60^\circ-75^\circ$ triangles that can tile some rectangle? In other words, from all tilings of rectangles with such triangles, I am looking for the one with the smallest number of triangles.

Dmitry Kamenetsky
  • 2,015

1 Answers1

12

enter image description here

Here's my 18-triangle solution.

From the coordinates, it seems the width/height ratio of the rectangle is 138/(96+6√₃) or (16-√₃)/11 which is about 1.297

How

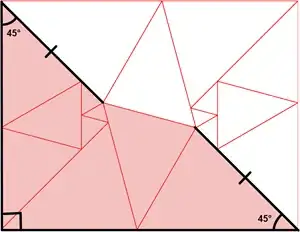
enter image description here

Using my code from answering this question, I checked for 5-sided polygons that have 45-degree, 90-degree, 45-degree angles in sequence, with equal lengths for the (parallel) "45-degree" sides.

I was happy to find that a simple solution exists!

Coordinates

27+6√₃,48+3√₃
63-9√₃,33+15√₃
36+8√₃,36+8√₃
27+6√₃,69
27+6√₃,27+6√₃
0,63-9√₃
0,96+6√₃
0,0
84-12√₃,0
75+9√₃,63-9√₃
138,0
111-6√₃,48+3√₃
102-8√₃,60-2√₃
111-6√₃,27+6√₃
111-6√₃,69
138,33+15√₃
138,96+6√₃
54+12√₃,96+6√₃
{{0,1,2},{3,1,0},{4,0,2},{5,4,3},{6,3,5},{7,5,4},{7,8,2},{8,9,1},{10,9,8},{11,9,12},{13,9,11},{14,11,12},{15,14,13},{10,13,15},{16,15,14},{16,17,12},{17,1,9},{6,1,17}}

Larger solutions

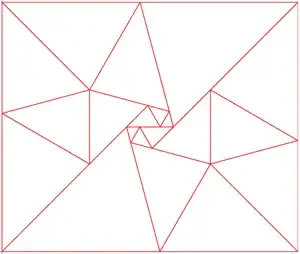
enter image description here

20 triangles (48 by 30+6√₃)

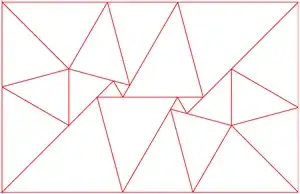
enter image description here

22 triangles (772 by 402+54√₃)

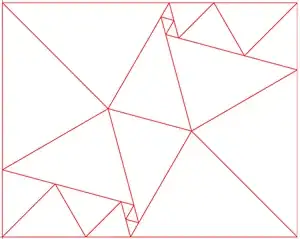
enter image description here

22 triangles (222 by 228-30√₃)

Tom Sirgedas
  • 1,028
  • 10
  • 12
  • Nice! This may not be minimal though. – markvs Nov 19 '21 at 02:09
  • Thanks! It's clear that at least 12 triangles are needed just to complete the perimeter, so proving a minimal solution might be within reach. – Tom Sirgedas Nov 19 '21 at 03:19
  • Perhaps. Is it clear that the number should be even? – markvs Nov 19 '21 at 03:24
  • Hmm, great question. I have no idea.

    I also wonder if you need exactly two interior vertices where 5 triangles meet.

     – Tom Sirgedas Nov 19 '21 at 03:42
  • (To clarify "at least 12 triangles are needed to complete the perimeter": each side of the rectangle needs at least one vertex (which will have 3 incident triangles), because a single triangle edge can't span an entire side of the rectangle. A triangle corner at a rectangle corner must be 45 degrees.) – Tom Sirgedas Nov 19 '21 at 04:01
  • 1
    I understood where $12$ came from. It is probably clear that the number is at least $14$. But the cases $15,16,17$ are not clear at all. – markvs Nov 19 '21 at 04:04
  • 1
    This is awesome, thank you Tom! – Dmitry Kamenetsky Nov 19 '21 at 06:37
  • Did you specifically search for symmetric solutions? Are there any non-symmetric solutions? – Dmitry Kamenetsky Nov 19 '21 at 10:25
  • I only searched for a special 5-sided polygon that covers exactly half the rectangle in a symmetrical way (see "How").

    Yeah, there a lot of ways to break symmetry. For example, any 45-60-75 triangle can be replaced with 4 smaller 45-60-75 triangles. Maybe the optimal solution for tiling a rectangle or square is non-symmetric.

     – Tom Sirgedas Nov 19 '21 at 17:28
  • re "I also wonder if you need exactly two interior vertices where 5 triangles meet": Yes!*

    Perimeter of square will have exactly 8 more 45-degree angles than 75-degree angles. So opposite must be true on interior, which can only be accomplished by two 75-75-75-75-60-degree "junctions".

    *Assuming you don't add 45-45-45-45 junctions along the square's perimeter.

     – Tom Sirgedas Nov 20 '21 at 05:38