Combo problem, complementary counting

Question

You have 5 blue nails in a column and 3 red nails in another column. You can attach a string between any red nail and blue nail. How many ways can we attach these strings such that every nail has at least 1 string attached to it?

For example, drawing all possible strings would work. Or connecting the first 3 blue with first 3 red, then connecting the last 2 blue to any red would work.

I approached this using Principle of Inclusion-Exclusion (if there is a simpler solution, let me know), but I am stuck. All I have is

$(2^5-1)^3$-something

$(2^5-1)^3$ is the number of non-empty subsets of blue nails for the red nails to connect to, cubed because 3 red nails. I don't know what to subtract from this though

Answer 1

Represent the connected pairs of nails in a $5\times3$ grid, where an $S$ in row $i$ and column $j$ represents a string between the $i$-th blue nail and the $j$-th red nail.

For example, here’s collection that you would want to count, because every nail has at least one string connected to it.

So if I understood your question correctly, you want to count the number of ways to place $S$’s in the grid so that no row or column is $S$-less. Equivalently, you want to count the number of $5\times3$ matrices containing $0$s and $1$s with no row or column that is all zeroes.

That question has been answered in general here, and as you and others recognize, it relies on the inclusion-exclusion principle.

Number of $(0,1)$ $m\times n$ matrices with no empty rows or columns

Answer 2

To figure out what to subtract, figure out what you've counted that you don't want to count.

You've counted every configuration that uses all 3 red nails, but you've included configurations that don't use all the blue nails. So count those (e.g. the ones that use only four blue nails) and subtract them. Using the inclusion-exclusion principle, you can correctly account for the configurations that use 3 blue nails, etc.

Note that this will be easier if you do it in the other direction, with cases based on the number of red nails used.

Answer 3

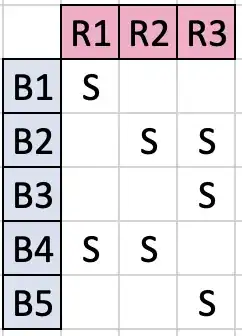
There are $5\cdot3=15$ blue-red pairs and a string can be there or not there; so the number of "stringings" from $5$ nails to $3$ nails is $2^{15}$. But this includes stringings which miss nails.

---

Inclusion-Exclusion

Let us call the subset of stringings that do not touch the $k^\text{th}$ red nail $R_k$ and the subset of stringings that do not touch the $k^\text{th}$ blue nail $B_k$. These are the $S_k$'s of the Generalized Inclusion-Exclusion Principle.

We can sum the sizes of the intersections of $k$ of the $B$'s and $R$'s ($N(k)$ from the Generalized Inclusion-Exclusion Principle): $$ N(k)=\sum_{j=0}^k\overset{\substack{\text{the number}\\\text{of choices}\\\text{of the $B$'s}\\\downarrow\\[3pt]\,}}{\binom{5}{j}}\overset{\substack{\text{the number}\\\text{of choices}\\\text{of the $R$'s}\\\downarrow\\[3pt]\,}}{\binom{3}{k-j}}\overbrace{2^{(5-j)(3-k+j)}\vphantom{\binom52}}^{\substack{\text{number of stringings}\\\text{given the choice of}\\\text{$B$'s and $R$'s}}}\tag1 $$ The number of stringings in $0$ of the $B$'s and $R$'s is given by the Generalized Inclusion-Exclusion Principle as $$ \sum_{k=0}^8(-1)^kN(k)%=16081 \tag2 $$

---

Simplification $$ \begin{align} f(a,b) &=\sum_{k}(-1)^kN(k)\tag{3a}\\ &=\sum_{j,k}(-1)^k\binom{a}{j}\binom{b}{k-j}2^{(a-j)(b-k+j)}\tag{3b}\\ &=\sum_{j,k}(-1)^{k+j}\binom{a}{j}\binom{b}{k}2^{(a-j)(b-k)}\tag{3c}\\ &=\sum_{j,k}(-1)^{a+b-k-j}\binom{a}{j}\binom{b}{k}2^{jk}\tag{3d}\\ &=\sum_{j}(-1)^{a-j}\binom{a}{j}\left(2^j-1\right)^b\tag{3e}\\ \end{align} $$ Explanation:
$\text{(3b)}$: plug $(1)$ into $(2)$
$\text{(3c)}$: substitute $k\mapsto k+j$
$\text{(3d)}$: substitute $j\mapsto a-j$ and $k\mapsto b-k$
$\text{(3e)}$: apply the Binomial Theorem

This is symmetric in $a$ and $b$, so take $a\le b$ to reduce the number of terms. $$ f(3,5)=\sum_{j=0}^3(-1)^{3-j}\binom{3}{j}\left(2^j-1\right)^5\tag4 $$ However, if we switch them around, we get $$ f(5,3)=\sum_{j=0}^5(-1)^{5-j}\binom{5}{j}\left(2^j-1\right)^3\tag5 $$ the $j=5$ term of which looks more like what is mentioned in the question.

---

Interpretations of the Simplified Formulas

In formula$(4)$, the index $j$ term counts the number of functions from the $5$ blue nails to a nonempty $j$-subset of the $3$ red nails, i.e. $\left(2^j-1\right)^5$, times the number of such $j$-subsets, i.e. $\binom{3}{j}$.

In formula$(5)$, the index $j$ term counts the number of functions from the $3$ red nails to a nonempty $j$-subset of the $5$ blue nails, i.e. $\left(2^j-1\right)^3$, times the number of such $j$-subsets, i.e. $\binom{5}{j}$.

Thus, $(2)$, $(4)$, and $(5)$ give three different ways to solve this problem (all using inclusion-exclusion).