Why is $0^0$ undefined and how would we graph this?

Question

So I saw exponents like $3^0$ and $4^0$, etc which are all equal to $1$.

And then soon I see that $0^0$ is not defined.

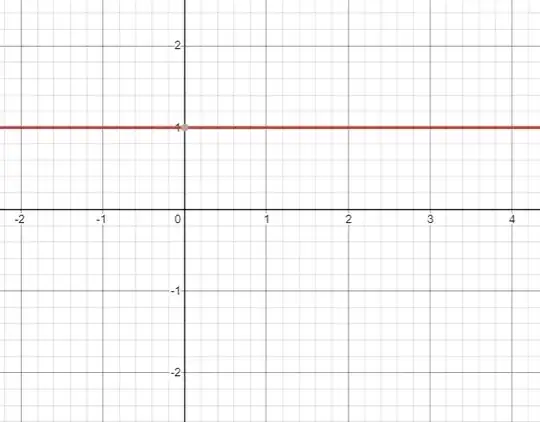
I checked the graph of $x^0$

Then I decided to make some observations.

We go like this:

$0.9^{0.9} = 0.909532576$

$0.8^{0.8} = 0.836511642$

$0.7^{0.7} = 0.779055912$

$0.6^{0.6} = 0.73602192281$

$0.5^{0.5} = 0.70710678118$

$0.4^{0.4} = 0.69314484315$

And then comes the moment:

$0.3^{0.3} = 0.69684530193$

And then, so on the values increase, and then finally the calculator breaks at $0.00000000000001^{0.000000000000001}$ and gives $1$.

I'd like to understand why $0.3^{0.3}$ is greater than $0.4^{0.4}$. And why the values go on increasing as we go $<0.3$.

So we get $\lim_{x\to 0} x^{x} = 1$.

Another amazing graph:

This thing has really intrigued me, and I wonder if there are more ways to prove that $0^0$ is undefined. Sharing more methods for the same would be highly appreciated!

Answer 1

I don't entirely agree that $0^0$ "is not defined". By definition of "define", you can define something to be whatever you want... some definitions turn out to be more helpful than others, though. There are lots of things in mathematics that are defined in some contexts and not in others. For instance, you will often have heard that something like $\frac{1}{0}$ is undefined, and that it would be absurd to assign it any value. However, in many areas of mathematics, it makes perfect sense to "invent" some thing $\infty$ that equals precisely $\frac{1}{0}$. When we do this, we have to be precise about what properties our new thing has, so as to avoid making logical errors.

This Wikipedia page for $0^0$ tells us that "The most common possibilities are 1 or leaving the expression undefined". As you have demonstrated in the question, $1$ does indeed seem the most reasonable choice if we do want to define it.

For the sake of completeness, I will also include an informal proof that the limit of $x^x$ as $x$ tends to $0$ from above is indeed $1$. We will use standard properties of the natural logarithm $\log$. For any positive real $x$, we have $$ x^x = e^{\log(x^x)} = e^{x\log x}, $$ and therefore it suffices to show that $x\log x \to 0$ as $x\to 0^+$. To see this, consider the sequence $(\frac{1}{n})_{n\geq 1}$. We have $$ \frac{1}{n}\log(\frac{1}{n}) = -\frac{1}{n}\log(n), $$ which converges to $0$ as $n\to \infty$ (I won't prove this but it follows from elementary properties of logarithms, and you can probably Google it). Therefore, since $x\log x$ is continuous for $x>0$ and $\frac{1}{n}\to 0$ as $n\to \infty$, we have $x\log x \to 0$ as $x \to 0^+$ as required.

Answer 2

I'd like to understand why $0.3^{0.3}$ is greater than $0.4^{0.4}$. And why the values go on increasing as we go $<0.3$.

As mentioned in the comments you can set the derivative equal to zero to obtain the extreme point. Let $f(x)=x^x, >0$

$\ln(f(x))=x\cdot \ln(x)$

Differentiating. On the left side we use the chain rule.

$\frac1{f(x)}\cdot f'(x)=\ln(x)+1$

$f'(x)=f(x)\cdot (\ln(x)+1)$

$f'(x)=x^x\cdot (\ln(x)+1)$

Setting the derivative equal to zero.

$=x^x\cdot (\ln(x)+1)=0\Rightarrow \ln(x)+1=0$

$\ln(x)=-1\Rightarrow x_E=\frac1e$. And you see that $0.3<\frac1e<0.4$

It remains to show that this extreme point is a (relative) minimum. So we need the second derivative. Using the product rule and we get

$f''(x)=x^x\cdot \left(\frac1x+(\ln(x)+1)^2\right)$

$f''\left(\frac1e\right)>0 \Rightarrow x_E=\frac1e$ is a (relative) minimum.