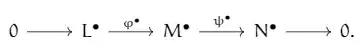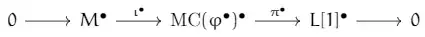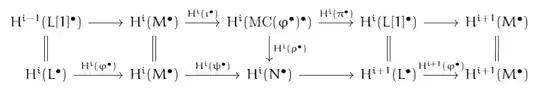Consider the following short exact sequence of complexes in an abelian category
Let $MC(\varphi^\bullet)^\bullet$ be the mapping cone of $\varphi^\bullet$. Recall that the mapping cone fits into an exact sequence
and that there's a natural quasi-isomorphism $\rho^\bullet:MC(\varphi^\bullet)^\bullet\to N^\bullet$, given by composing the projection with $\psi^\bullet$. Most books in homological algebra (Proposition IX.4.1 in Aluffi's Algebra: Chapter 0, for example) affirm that the connecting morphism $H^i(L^\bullet)\to H^i(M^\bullet)$ coincides with $H^i(\varphi^\bullet)$. I wonder what this even means. As in Uniqueness of the connecting morphism in the snake lemma, the connecting morphisms are not really unique. Since we only know that there exists connecting morphisms, does it even make sense to say that, paraphrasing Aluffi, "the connecting morphism is the morphism induced by $\varphi^\bullet$ in cohomology"?
If this indeed makes sense, is it also true that the diagram
commutes?