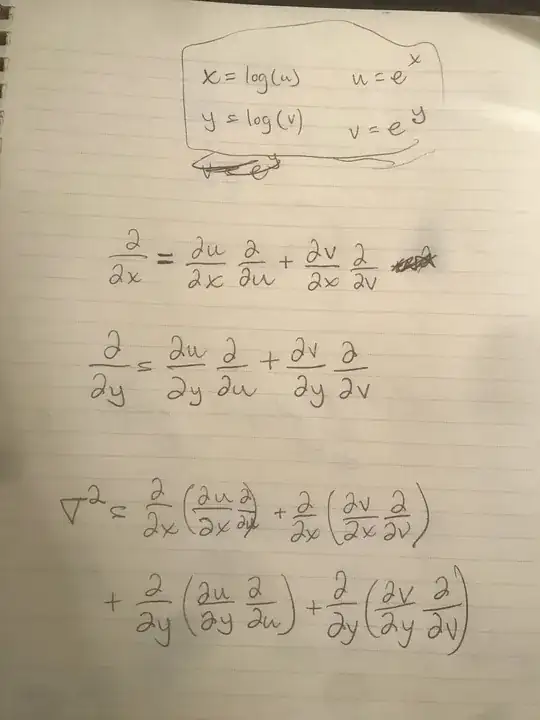0

I am working on becoming more agile using different coordinates to solve problems.

Depending on which coordinates one uses the "Laplacian" takes different forms:

Coordinate expressions for the Laplacian

I have (1) watched online tutorials (2) read the wikipedia section, and tried to use the information I know to express the "Laplacian" in $u-v$ coordinates s.t. $u=e^x$ and $v=e^y.$

How do you write the "Laplacian" in $u-v$ coordinates?

I understand pretty well the conversion of the "Laplacian" from cartesian to cylindrical coordinates. I don't quite understand the conversion for a less used coordinate system such as the $u-v$ one.

Here's my attempt:

enter image description here

John Zimmerman
  • 1,070
  • Please show your attempt. – Kavi Rama Murthy Feb 27 '21 at 09:59
  • okay I am going to edit the post and show my attempt okay? – John Zimmerman Feb 27 '21 at 10:02
  • 1
    Please write the text in latex ^^ – tryst with freedom Feb 27 '21 at 10:20
  • 1
    Ok, now notice that $\frac{\partial u}{\partial x}=e^x = u$ and $\frac{\partial v}{\partial x}=0$; make these simplifications as you go along. From here, just carry on with your calculation and replace all instances of $\frac{\partial}{\partial x}$. I found $\nabla^2f=u\frac{\partial}{\partial u}\left(u\frac{\partial f}{\partial u}\right) + v\frac{\partial}{\partial v}\left(v\frac{\partial f}{\partial v}\right)$ (though I admit, I just used the general formula for the Laplacian in an arbitrary coordinate system to arrive at this result). – peek-a-boo Feb 27 '21 at 10:37

1 Answers1

1

Here is a hint: $$ \frac{\partial}{\partial x}( \frac{\partial u}{\partial x} \frac{\partial f(u,v)}{\partial u}) = \frac{\partial^2 u}{\partial x^2} \frac{\partial f}{\partial u} +( \frac{\partial u}{\partial x} ) \frac{\partial}{\partial x}\left[ \frac{\partial f}{\partial u} \right]$$

Now,

$$ \frac{\partial }{\partial x} (\frac{\partial f}{\partial u}) = [\frac{\partial u}{\partial x} \frac{\partial^2 f}{\partial u^2} + \frac{\partial v}{\partial x} \frac{\partial^2 f } {\partial v \partial u}] \tag{1}$$

To understand this, consider $ \frac{\partial f}{\partial u} = g(u,v)$ then,

$$ \frac{\partial }{\partial x} g(u,v) = \left[ \frac{\partial u}{\partial x} \frac{\partial g}{\partial u} + \frac{\partial v}{\partial x} \frac{\partial g}{\partial v} \right]$$

And then plug back in $ g(u,v) = \frac{\partial f}{\partial u}$

And plug that back in. It's much more easier to track the dependencies when you have an actual function attached than to work with abstract operators. A comment on (1) is that it reminiscent of the parameteric derivative: $$ \frac{dy}{dx} = \frac{dt}{dx} \frac{dy}{dt}$$

Or, in operator form:

$$ \frac{d}{dx} = \frac{dt}{dx} \frac{d}{dt}$$

The 'trouble' comes when we try to compose the operator that is:

$$ \frac{d^2}{dx^2} = \frac{dt}{dx} \frac{d}{dt} ( \frac{dt}{dx} \frac{d}{dt})$$

The right hand simplfies too:

$$ \frac{dt}{dx} \left[ \frac{d}{dt} (\frac{dt}{dx}) + \frac{d^2 }{dt^2}\right]$$

The confusing term at hand is $ \frac{d}{dt} \frac{dt}{dx}$ similar to $ \frac{\partial}{\partial x}\left[ \frac{\partial f}{\partial u} \right]$ [see here]

tryst with freedom
  • 11,538