Recently I have been studying parametric equations of surfaces and curves, specifically hyperbolic functions. Given by the equations $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1, \quad\frac{(x-\alpha)^2}{a^2}-\frac{(x-\beta)^2}{b^2}=1$$
denoting hyperbolic functions centred at $(0,0)$ and $(\alpha,\beta)$ respectively. I am however, unable to derive a parametrisation that represents the entire function. Help to further understand this topic would be greatly appreciated.
Here's a geometric way to derive a parametrization. Consider the family of all lines passing through the point $(a,0)$. Such a line is of the form $y = t(x-a)$ for some slope $t$. Since the hyperbola has degree $2$, each line will intersect it in exactly two points: $(a,0)$ and one other point. (This is an example of Bézout's Theorem.) As we vary the slope $t$, this other point will trace out the curve.
Let's use this observation to compute equations for the parametrization. Substituting $y = t(x-a)$ into the equation for the hyperbola, we have \begin{align*} 0 &= \frac{x^2}{a^2} - \frac{y^2}{b^2} - 1 = \frac{x^2}{a^2} - \frac{(t(x-a))^2}{b^2} - 1 \, . \end{align*} Multiplying through by $a^2 b^2$ to clear denominators yields \begin{align*} 0 &= b^2 x^2 - a^2 (t(x-a))^2 - a^2 b^2 = b^2 x^2 - a^2 t^2(x^2 - 2ax + a^2) - a^2 b^2\\ &= (b^2 - a^2 t^2)x^2 + 2 a^3 t^2 x - a^4t^2 - a^2 b^2 \end{align*} and dividing through by the leading coefficient, we find $$ 0 = x^2 + \frac{2 a^3 t^2}{b^2 - a^2 t^2} x - \frac{a^2 (a^2 t^2 + b^2)}{b^2 - a^2 t^2} \, . $$
One of the roots is $x = a$ and since the constant term is the product of the roots, then the other is \begin{align*} x = -\frac{a (a^2 t^2 + b^2)}{b^2 - a^2 t^2} \end{align*} which, together with $$ y = t(x-a) = t\left(-\frac{a (a^2 t^2 + b^2)}{b^2 - a^2 t^2} - a\right) $$ gives a parametrization of the whole hyperbola, except for the point $(a,0)$. Note that since $b^2 - a^2 t^2 = (b - at)(b+at)$, then $x$ and $y$ have poles at $t = b/a$ and $t=-b/a$. Here's a SageMath cell plotting this parametrization, and the resulting plot with the ranges $t < -b/a$, $-b/a < t < b/a$, and $b/a < t$ colored differently.
$\hspace{4cm}$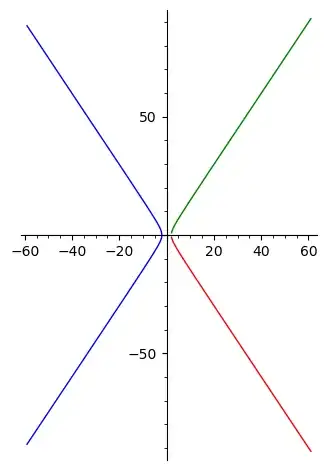 
For more on parametrizing curves, see Ch. $1$, $\S3$ of Cox, Little, and O'Shea's Ideals, Varieties, and Algorithms. It's a wonderful book, and they use fun examples like this to motivate later topics in the book.
General equation of conic section : $$ax^2+2bxy+cy^2+2dx+2fy+g=0$$ with constant coefficients $a,b,c,d,f,g$.
The curve is an hyperbola if : $$b^2-ac>0\quad;\quad a\neq 0 \quad;\quad c\neq 0$$ For parametrisation see : https://mathworld.wolfram.com/QuadraticCurve.html
